リバース量子アニーリングを用いたポートフォリオ最適化

リバース量子アニーリングを用いたポートフォリオ最適化#

はじめに#

この章ではポートフォリオ最適化問題を例として、OpenJijを用いてリバース量子アニーリング（Reverse Quantum Annealing）という、古典的な最適化計算と、量子アニーリングを組み合わせた手法を紹介します。このチュートリアルでは、古典的なアルゴリズム、普通の量子アニーリング、そしてリバース量子アニーリングそれぞれで同じポートフォリオ最適化問題を解き、その結果を比較します。またその過程を通して、OpenJijでの量子アニーリングの実装や実験を行う時の注意点についても触れていきます。

注意：このポートフォリオの内容を正しく実行するにはOpenJij0.4.9以上が必要です。必要な場合は実行前に次のコマンドを実行し、OpenJijのアップデートを行なってください。

pip install -U openjij

ポートフォリオ最適化問題#

資産運用のための投資活動を行うとき、誰しも「できるだけリスクを回避しながら大きな収益を実現させたい」と考えるはずです。よって収益が限定的ですが、リスクが小さい（ないし全くない）資産と、見込める収益が大きい分リスクも大きい資産を組み合わせてポートフォリオを作り、分散投資を行うのが一般的な戦略となります。

この時、与えられた一定のリスクでは最大利益を実現したい、または同じ利益を実現する場合にできるだけ小さいリスクを取るには、最適なポートフォリオを選ぶ必要があります。現在、よく利用される手法にMarkowitzによる現代ポートフォリオ理論(Modern Portfolio Theory)があります。ポートフォリオを構成する銘柄の間の相関を考慮し、その共分散を最小にすることを目指す手法です[1]。

\min \sum_{i=1}^{N}\sum_{j=1}^{N}w_{i}w_{j}\sigma_{ij}; \quad \sum_{i=1}^{N}W_{i}=1; \quad \sum_{i=1}^{N}W_{i}\mu_{i}=R

$w_{i}$ は各銘柄がポートフォリオ内に占める重み、 $\sigma_{ij}$ は銘柄間の共分散を表します。 $\mu_{i}$ は各銘柄の期待収益で、 $R$ はこのポートフォリオの総収益です。

この時、ポートフォリオのパフォーマンスの評価によく使われる指標としてSharpe Ratioというものがあります。

Sharpe Ratio#

Sharpe Ratioは投資の効率性を評価する指標で、銘柄単体とポートフォリオに対して計算されます。1966年にウィリアム・シャープによって提案されました[3]。その基本的な定義を以下に示します。

S = \frac{\bar{r}-r_0}{\sigma}

ここで $\bar{r}$ は一定時間内の平均的なリターン率で、月間や年間リターンの平均を利用することが多くあります。 $r_0$ はリスクなしの場合のリターン率を表し、普段は安定した国債の利子率などを用います。そして $\sigma$ は資産価値の変動の激しさを意味するボラティリティです。

実際にSharpe Ratioを計算するときには、場面によって異なる計算方法でこれらの値を算出します。例えばリターンは単純リターンとして $r=P(t+1)/P(t) - 1$ で資産価格 $P$ を使って計算される場合と、 $r=log[P(t+1)/P(t)]$ のように対数リターン率として計算される場合が存在します。そしてボラティリティも価格の変動から計算する手法とリターン率からの計算するやり方があります。具体的に興味がある方は金融工学や市場分析などに関連する本とサイトに参照すると良いでしょう。

ポートフォリオの評価と最適化#

Sharpe Ratioの定義から、その値が大きいということは収益が大きいまたはリスク（ボラティリティ）が小さいことを意味します。ある与えられた銘柄の集合から作られたポートフォリオのうち、最大のSharpe Ratioを実現できるような組合せは、単位リスクに対して最大のリターンを得る組み合わせと言えます。よってポートフォリオの最適化問題が一定の考え方の元では、Shape Ratioを最大化する問題に置き換えることができます。

現実では、この最適化は銘柄を選別した上で、それぞれの銘柄に投入する資金の量を決定しなければなりません。すなわち、これは選ぶ銘柄と各銘柄のウェイトを決定する組合せ最適化問題となります。このチュートリアルは、参考にした論文[2]に従い、簡単のために各銘柄のウェイトを等しくする戦略について考えます。 $M$ 個ある銘柄のうち $N$ 個銘柄を選び出し、Sharpe Ratioを最大にする組合せを求めます。すると、次のようなQUBO形式に問題を翻訳することができます。

\mathcal{O}(\boldsymbol{q})=\sum_{i=1}^{N}a_{i}q_{i}+\sum_{i=1}^{N}\sum_{j=i+1}^{N}b_{ij}q_{i}q_{j}

ここで $q_{i}$ は各銘柄に対する選択を表すバイナリ変数で、 $1$ であればポートフォリオに組み入れ、 $0$ であれば組み入れないことを意味します。 $a_i$ は銘柄自体のパフォーマンスによる魅力スコアであり、 $b_{ij}$ は銘柄間のペアワイズ相関で決められた罰金または賞金の度合を表します。

具体的に $a_i$ と $b_{ij}$ は次の表1に従って決定されます。

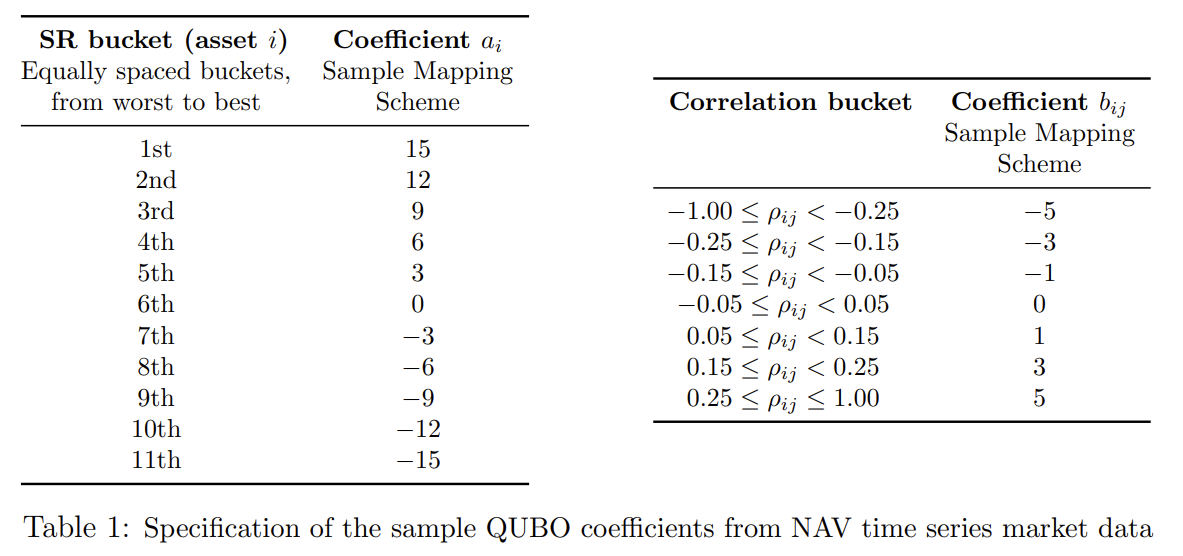
../../../_images/reverse_annealing_RQA_QUBO.png

この表の $a_i$ のグループは、ポートフォリオを構成する人によって決められた基準であり、銘柄を魅力的であるものから順に並べられたものです。それらを順位付けした後に、均等に分けた場合に形成されたグループを示しています。この魅力的な基準はリターン率の高さなどの要素も取り入れられますが、このチュートリアルでは単純に銘柄単体のSharpe Ratio順を用いています。次の $b_{ij}$ は対数リターンの時系列から求められた相関行列の成分 $\rho_{ij}$ の値によって決められたものです。

このQUBOを用いて量子アニーリングを実行すれば、最適なポートフォリオを得ることができるはずです。また、選択銘柄の数について指定したい場合は、銘柄数に対して制約条件を付け加えます。ただし、参考にした論文[2]によると、制約条件を罰金法でQUBOに付け加えた場合、導入した大きい相互作用（ペナルティ）はアニーリング性能や最終的に取得した結果にも影響することが示されています。現実の問題では、最適なポートフォリオに含まれる銘柄の数は分からないため、このチュートリアルでも同様に銘柄数制限なしての最適化を行います。

Reverse Quantum Annealingによるポートフォリオ最適化#

現実のポートフォリオ最適化の問題は基本、大きな銘柄数を持つ市場からいくつかの銘柄を選択することになります。候補銘柄数が増加すると、最適なポートフォリオを作るための計算量も大きくなります。よって一定の条件の下に選別を行い、その次に最適化アルゴリズを適応するのが一般的です。そして、銘柄の組合せの自由度から、最終的に実現したSharpe Ratioが最大Sharpe Ratioと極めて近い値を持つような局所解が多く存在することもあり得ます。伝統的なアルゴリズムがそのようなエネルギーランドスケープの谷に囚われた場合、そこから抜け出すのにも時間とリソースが必要となります。そのため、以上の既存の問題点を回避しつつポートフォリオ最適化問題を解くには、量子アニーリングのような大きい数の相関を取り扱うことができ、かつ局所解から脱却できる計算手法の方が上手に解くことができます。

ただし参考論文[2]に示されたように、単純なForward Annealingのみを行う場合では、銘柄数の増加により、最適解までにたどり着く時間も大きく増加します。結果としてこれまでの遺伝的アルゴリズムと近いパフォーマンスになることが判明しています。その理由としては先述の通り、最適解と近い値のSharpe Ratioを持つ解と最適解はエネルギーの違いが小さく、最適解へのエネルギー変化がほぼない準位間に高いポテンシャル障壁があるような遷移となるため、遷移が起こるまでにより長い時間が必要となるためでし。また量子アニーリングマシン実機では、通常のアニーリングを行う途中で熱ノイズなどにより系が励起されて時間発展する場合があります。これらの要因により、最終結果が最適解とならないこともあります。

Reverse Quantum Annealing#

これら量子アニーリングを用いた時の問題点を解決するために提案された手法の一つに、Reverse Quantum Annealingがあります。名前通り、通常のForward Annealingと逆方向のステップを導入するような量子アニーリングを実行することを意味します。通常のForward Annealingの時間依存のハミルトニアンは次のように書かれます。

\mathcal{H}_{\mathrm{QA}}(t)=A[t]\sum_{i=1}^N\sigma_{i}^{\mathrm{x}}+B[t]\mathcal{H}_{\chi-\mathrm{Ising}}

ここで $A[t]$ はアニーリングを行うとき系にかける横磁場の大きさ、 $B[t]$ は問題のハミルトニアン $\mathcal{H}_{\chi-\mathrm{Ising}}$ の振幅を表します。次の図でのa)で示されるように、Forward Annealingの場合はアニーリングの進行に従って、 $A[t]$ を徐々に小さくし、同時に $B[t]$ を支配的にさせていきます。アニーリング完了時では $A[t]=0$ となります。

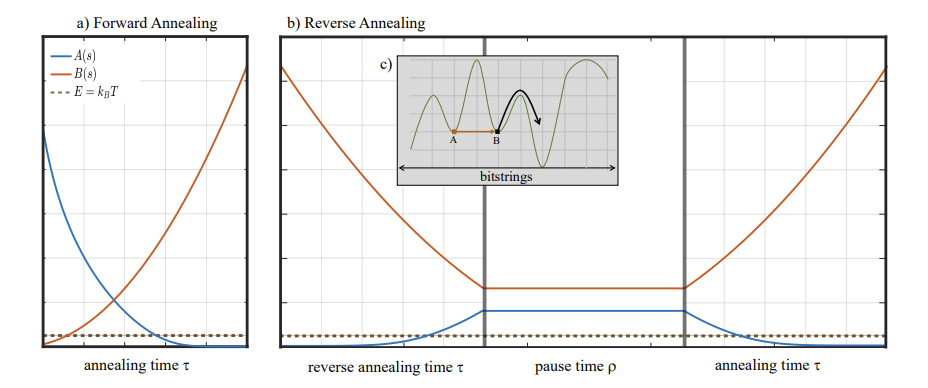
../../../_images/reverse_annealing_QAandRQA.png

それに対し、Reverse Annealingはb)のように $A[t]=0,B[t]=1$ の状態から出発します。このとき、まず通常とは逆に $B[t]$ を小さくしていきます。これをReverse Phaseと呼びます。この段階では系のエネルギーが逆に高くなるため、c)に示されているようなAB間のポテンシャル障壁を越えやすくなります。そして $A[t], B[t]$ をある値に到達させた後、系をそのままの状態を維持してしばらく待ちます。これをPause Phaseと呼びます。この間も高いエネルギーの状態が維持されるため、熱的ホッピングが起こりやすい状況となります。するとBの右側のようなポテンシャル障壁も越えやすくなっています。これにより最初にいた局所解から脱し、最適解付近にたどり着く可能性が上がることが示唆されます。最後にまた $A[t]$ を小さくし、 $B[t]$ を大きくさせるForward Phaseで通常のアニーリングを実行することで、最適解を取得します。このプロトコルでは、Reverse phadeで $A[t], B[t]$ を停止させた値や、各段階での継続時間などにより、最終的に得られる解のパフォーマンスにも影響することが考えられます。

Reverse Quantum Annealingによるポートフォリオ最適化の手順#

ここまでの議論から、Reverse annealingではReverse Phaseの初期状態が必要です。ランダムに生成された初期状態を用いることも可能ですが、手法が提案された背景からもわかるように、ある種の局所解の状態を用意したほうが最適解探索の効率が向上することが予想されます。参考論文[2]では初期状態となる局所解を得るために、伝統的なアルゴリズムで得られた出力を利用しています。このチュートリアルもそれに従って、Revearse annealingを実行してみましょう。

以上から、これから行う実装は基本論文[2]の流れを参考にして以下のようになります。

最適化を行う銘柄データの生成
古典なアルゴリズムの実装とその結果の確認
通常のForward Annealingによる最適解探索
Reverse Quantum Annealingによる最適解探索
Reverse Quantum Annealingのパラメータ探索

銘柄データの生成と古典アルゴリズムの実装#

最適化を行う銘柄データの生成#

参考論文[2]にある方法に従い、与えられた初期値を用いて、ブラウン運動による銘柄チャートを生成します。

import numpy as np
import matplotlib.pyplot as plt
import random

#Magic numbers to generate assets
rho = 0.1 # input uniform correlation
mu = 0.075 # expected value
sigma = 0.15 # volatility/standard error
r0 = 0.015 # no risk return

参考論文[2]の付録Aから、各時刻においてチャートの運動は前時刻の運動を用いて

S(t_{n+1})=S(t_n)\exp(\mu-\frac{1}{2}\sigma^2)\Delta t + \sigma Z_n\sqrt{\Delta t}

のように与えられます。ここで $Z_n$ はCholesky分解で作られた一様相関行列 $\rho$ を従う多変量正規分布です。

これを実行し、チャートをプロットして様子を確認しましょう。初期に同じ価値から始め12ヶ月の推移を見ると、全体が広がっていく様子がわかります。一部銘柄では大きく上昇または降下する振る舞いも確認できます。

#相関正規確率変数Znの生成
def createZvariables(N, rho):
  rho_mat = np.full((N,N), rho)
  rho_mat[range(N), range(N)] = 1.0
  rho_chole = np.linalg.cholesky(rho_mat)
  zNs_temp = np.random.normal(0, 1, (10000, N))
  zNs = zNs_temp @ rho_chole
  return zNs

#チャートのブラウン運動の生成
def GetNextSt(St, mu, sigma, zN):
  Deltat = 1
  scale = np.exp((mu-0.5*sigma*sigma)*Deltat + sigma*zN*np.sqrt(Deltat))
  NextSt = St * scale
  return NextSt

Nassets = 48 #生成する銘柄の数
chart = list()
ZList = list()
Zvariables = createZvariables(Nassets, rho)
Zlabels = random.sample([x for x in range(10000)], 12) #Z variable shuffle

for label in Zlabels:
  ZList.append(Zvariables[label])

for iasset in range(Nassets):
  chart_asset = [1.0] #初値 相対価格で1.0

  #12ステップ（か月）シミュレーションを行う
  for month in range(12):
    chart_asset.append(GetNextSt(chart_asset[month], mu, sigma, ZList[month][iasset]))

  chart.append(chart_asset)
  #print(chart_asset) #各銘柄の具体的な数値をプリント
  plt.plot(list(range(13)), chart_asset)

plt.xlabel("Month", loc="right")
plt.ylabel("Relative Price", loc="top")
plt.show()

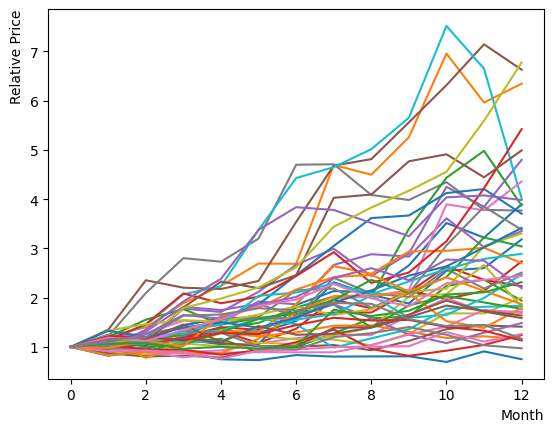
../../../_images/85839b0397f2c39e9a1a3a3f58df386789e3db237624684ad7fc0484ef013086.png

次に各銘柄のSharpe Ratioを計算します。ここでは先程の結果を評価するに実現Sharpe Ratioを用います。その定義に従い、無リスク利回り率を超過した超過収益率の平均 $\bar{r}$ と超過リターン率の標準偏差 $\sigma$ から求めましょう。チャートの確認から判明したように、銘柄数が少ない場合は偶然による偏りが大きい・生成条件に銘柄間の相関による影響があるため、銘柄を100回生成しその平均Shape Ratioを確認することでそれらの影響を減らします。結果として、銘柄の平均Sharpe Ratioが期待通り $0.4$ になるのが確認できます。またSharpe Ratioの計算定義を変更した場合には、当然Sharpeの値が変化することが確認できますが、おおむね $0.40\pm0.05$ の範囲内には収まることもわかります。

#銘柄生成関数
def CreateAssets(Nassets): 
  chart = list()
  ZList = list()
  Zvariables = createZvariables(Nassets, rho)
  Zlabels = random.sample([x for x in range(10000)], 12)
  for label in Zlabels:
    ZList.append(Zvariables[label])
  for iasset in range(Nassets):
    chart_asset = [1.0]
    for month in range(12):
      chart_asset.append(GetNextSt(chart_asset[month], mu, sigma, ZList[month][iasset]))
    chart.append(chart_asset)
  return chart

#オーソドックスなSharpe Ratio
def CalculateSharpeRatio(asset):
    monthly_return = list()
    for month in range(12):
      valueChange = asset[month+1]/asset[month] - 1.0 - r0
      monthly_return.append(valueChange)

    annualized_excess_return = np.mean(monthly_return)
    volatility = np.std(monthly_return, ddof=1)

    return(annualized_excess_return/volatility)

#log-returnに基づいたSharpe Ratio
def CalculateSharpeRatio_log(asset):
  monthly_log_return = list()
  for month in range(12):
    valueChange = np.log(asset[month+1]/asset[month])
    monthly_log_return.append(valueChange)
  mean_log_return = np.mean(monthly_log_return)
  volatility = np.std(monthly_log_return, ddof=1)

  return (mean_log_return-r0)/volatility

#少し変わった定義のSharpe Ratio
def CalculateSharpeRatio_2(asset):
  monthly_log_return = list()
  monthly_return = list()
  for month in range(11):
    log_valueChange = np.log(asset[month+1]/asset[month])
    monthly_log_return.append(log_valueChange)
    valueChange = asset[month+1]/asset[month] - 1.0
    monthly_return.append(valueChange)
  annualized_excess_return = np.mean(monthly_return) - r0
  volatility = np.std(monthly_log_return, ddof=1)

  return (annualized_excess_return/volatility)

allmean = 0
for ntry in range(100): #複数回試行で同じセットないの相関による影響を消す
  Chart = CreateAssets(48) #指定した数の銘柄を作る
  mean_SR = 0.0
  n = 0.
  for asset in Chart:
    assetSR = CalculateSharpeRatio(asset) #ここを変更すればShape Ratioの計算方法を変えられる
    #assetSR = CalculateSharpeRatio_log(asset)
    #assetSR = CalculateSharpeRatio_2(asset)
    mean_SR = ((mean_SR*n)+assetSR) / (n+1) #平均Shape Ratio
    n+=1
  print("SubSet "+ str(ntry)+ " average Sharpe Ratio: " + str(mean_SR))
  allmean = ((allmean*ntry)+mean_SR) / (ntry+1)
  print("Average Sharpe Ratio of all generated: "+ str(allmean))

SubSet 0 average Sharpe Ratio: 0.48858266597546907
Average Sharpe Ratio of all generated: 0.48858266597546907
SubSet 1 average Sharpe Ratio: 0.29839160286029087
Average Sharpe Ratio of all generated: 0.39348713441787997
SubSet 2 average Sharpe Ratio: 0.43962543144174093
Average Sharpe Ratio of all generated: 0.40886656675916694
SubSet 3 average Sharpe Ratio: 0.3640886094948434
Average Sharpe Ratio of all generated: 0.3976720774430861
SubSet 4 average Sharpe Ratio: 0.4865545699984157
Average Sharpe Ratio of all generated: 0.41544857595415197
SubSet 5 average Sharpe Ratio: 0.530860399486304
Average Sharpe Ratio of all generated: 0.43468387987617735
SubSet 6 average Sharpe Ratio: 0.3570374063582336
Average Sharpe Ratio of all generated: 0.4235915265164711
SubSet 7 average Sharpe Ratio: 0.369115114238696
Average Sharpe Ratio of all generated: 0.41678197498174924
SubSet 8 average Sharpe Ratio: 0.4943521578889212
Average Sharpe Ratio of all generated: 0.42540088419365724
SubSet 9 average Sharpe Ratio: 0.22536548023691738
Average Sharpe Ratio of all generated: 0.4053973437979833
SubSet 10 average Sharpe Ratio: 0.4981202188264873
Average Sharpe Ratio of all generated: 0.41382669607330186
SubSet 11 average Sharpe Ratio: 0.4421885675926663
Average Sharpe Ratio of all generated: 0.4161901853665822
SubSet 12 average Sharpe Ratio: 0.30801521475672394
Average Sharpe Ratio of all generated: 0.4078690337812085
SubSet 13 average Sharpe Ratio: 0.4955218286787302
Average Sharpe Ratio of all generated: 0.41412994770246003
SubSet 14 average Sharpe Ratio: 0.4411961573623984
Average Sharpe Ratio of all generated: 0.41593436167978926
SubSet 15 average Sharpe Ratio: 0.3915424891386621
Average Sharpe Ratio of all generated: 0.4144098696459688
SubSet 16 average Sharpe Ratio: 0.3375742026900776
Average Sharpe Ratio of all generated: 0.4098901245309164
SubSet 17 average Sharpe Ratio: 0.4796928297159821
Average Sharpe Ratio of all generated: 0.41376805259675337
SubSet 18 average Sharpe Ratio: 0.5423449042304876
Average Sharpe Ratio of all generated: 0.42053525531431835
SubSet 19 average Sharpe Ratio: 0.4189093891843179
Average Sharpe Ratio of all generated: 0.4204539620078183
SubSet 20 average Sharpe Ratio: 0.34174212003603527
Average Sharpe Ratio of all generated: 0.41670577905678097
SubSet 21 average Sharpe Ratio: 0.3996654922322525
Average Sharpe Ratio of all generated: 0.41593122056475695
SubSet 22 average Sharpe Ratio: 0.5355237158775755
Average Sharpe Ratio of all generated: 0.4211308942740099
SubSet 23 average Sharpe Ratio: 0.33465418687276793
Average Sharpe Ratio of all generated: 0.4175276981322915
SubSet 24 average Sharpe Ratio: 0.5351007249023657
Average Sharpe Ratio of all generated: 0.42223061920309446
SubSet 25 average Sharpe Ratio: 0.296924718367466
Average Sharpe Ratio of all generated: 0.4174111614786472
SubSet 26 average Sharpe Ratio: 0.5406257958517272
Average Sharpe Ratio of all generated: 0.42197466645542797
SubSet 27 average Sharpe Ratio: 0.37371136367642577
Average Sharpe Ratio of all generated: 0.4202509770704636
SubSet 28 average Sharpe Ratio: 0.5076173340321266
Average Sharpe Ratio of all generated: 0.42326361006914165
SubSet 29 average Sharpe Ratio: 0.4219007620837942
Average Sharpe Ratio of all generated: 0.4232181818029634
SubSet 30 average Sharpe Ratio: 0.4419562674681585
Average Sharpe Ratio of all generated: 0.42382263617926
SubSet 31 average Sharpe Ratio: 0.5529641861125808
Average Sharpe Ratio of all generated: 0.4278583096146763
SubSet 32 average Sharpe Ratio: 0.42661645320572655
Average Sharpe Ratio of all generated: 0.42782067760228387
SubSet 33 average Sharpe Ratio: 0.396440664583307
Average Sharpe Ratio of all generated: 0.4268977360429022
SubSet 34 average Sharpe Ratio: 0.41985112257492635
Average Sharpe Ratio of all generated: 0.4266964042295315
SubSet 35 average Sharpe Ratio: 0.345995968789957
Average Sharpe Ratio of all generated: 0.42445472546732105
SubSet 36 average Sharpe Ratio: 0.412616578906329
Average Sharpe Ratio of all generated: 0.42413477556026724
SubSet 37 average Sharpe Ratio: 0.44287531909074707
Average Sharpe Ratio of all generated: 0.42462794775843776
SubSet 38 average Sharpe Ratio: 0.21686898893422132
Average Sharpe Ratio of all generated: 0.4193007949680732
SubSet 39 average Sharpe Ratio: 0.3799607825059834
Average Sharpe Ratio of all generated: 0.4183172946565209
SubSet 40 average Sharpe Ratio: 0.5343583522539276
Average Sharpe Ratio of all generated: 0.4211475643540187
SubSet 41 average Sharpe Ratio: 0.43490785782921376
Average Sharpe Ratio of all generated: 0.42147519038914233
SubSet 42 average Sharpe Ratio: 0.4168061274016414
Average Sharpe Ratio of all generated: 0.42136660752896793
SubSet 43 average Sharpe Ratio: 0.42767934937321145
Average Sharpe Ratio of all generated: 0.4215100789345189
SubSet 44 average Sharpe Ratio: 0.40431404978053687
Average Sharpe Ratio of all generated: 0.42112794495331934
SubSet 45 average Sharpe Ratio: 0.46657725989431514
Average Sharpe Ratio of all generated: 0.42211597353899316
SubSet 46 average Sharpe Ratio: 0.3055800572342023
Average Sharpe Ratio of all generated: 0.41963648595804015
SubSet 47 average Sharpe Ratio: 0.39206793200131673
Average Sharpe Ratio of all generated: 0.41906214108394174
SubSet 48 average Sharpe Ratio: 0.2683022616458889
Average Sharpe Ratio of all generated: 0.4159854088505121
SubSet 49 average Sharpe Ratio: 0.31102799671572096
Average Sharpe Ratio of all generated: 0.4138862606078163
SubSet 50 average Sharpe Ratio: 0.2728418367111248
Average Sharpe Ratio of all generated: 0.4111206836686655
SubSet 51 average Sharpe Ratio: 0.41348001110184934
Average Sharpe Ratio of all generated: 0.4111660553500729
SubSet 52 average Sharpe Ratio: 0.4212312508346699
Average Sharpe Ratio of all generated: 0.41135596469883884
SubSet 53 average Sharpe Ratio: 0.27852034022707567
Average Sharpe Ratio of all generated: 0.4088960457271395
SubSet 54 average Sharpe Ratio: 0.4642797975194151
Average Sharpe Ratio of all generated: 0.4099030230324536
SubSet 55 average Sharpe Ratio: 0.44134483880381276
Average Sharpe Ratio of all generated: 0.4104644840283707
SubSet 56 average Sharpe Ratio: 0.45397998515817767
Average Sharpe Ratio of all generated: 0.41122791387275326
SubSet 57 average Sharpe Ratio: 0.5549187293898966
Average Sharpe Ratio of all generated: 0.41370534172649714
SubSet 58 average Sharpe Ratio: 0.34268063723819314
Average Sharpe Ratio of all generated: 0.41250153317584787
SubSet 59 average Sharpe Ratio: 0.38501388563425715
Average Sharpe Ratio of all generated: 0.4120434057168214
SubSet 60 average Sharpe Ratio: 0.3055576181287514
Average Sharpe Ratio of all generated: 0.4102977370678367
SubSet 61 average Sharpe Ratio: 0.4789434592911323
Average Sharpe Ratio of all generated: 0.4114049261359543
SubSet 62 average Sharpe Ratio: 0.4825192379004444
Average Sharpe Ratio of all generated: 0.41253372473539063
SubSet 63 average Sharpe Ratio: 0.33057335713301317
Average Sharpe Ratio of all generated: 0.4112530939916035
SubSet 64 average Sharpe Ratio: 0.33005467342250056
Average Sharpe Ratio of all generated: 0.4100038875213096
SubSet 65 average Sharpe Ratio: 0.5113271493522311
Average Sharpe Ratio of all generated: 0.41153908845814174
SubSet 66 average Sharpe Ratio: 0.3034735799259123
Average Sharpe Ratio of all generated: 0.4099261704203473
SubSet 67 average Sharpe Ratio: 0.4862325970304608
Average Sharpe Ratio of all generated: 0.411048323752849
SubSet 68 average Sharpe Ratio: 0.38503694553720047
Average Sharpe Ratio of all generated: 0.41067134725697
SubSet 69 average Sharpe Ratio: 0.4035788826644005
Average Sharpe Ratio of all generated: 0.4105700263342191
SubSet 70 average Sharpe Ratio: 0.4458052742129845
Average Sharpe Ratio of all generated: 0.41106629743110307
SubSet 71 average Sharpe Ratio: 0.5907758196519679
Average Sharpe Ratio of all generated: 0.41356226301750393
SubSet 72 average Sharpe Ratio: 0.5030131753895352
Average Sharpe Ratio of all generated: 0.4147876179815044
SubSet 73 average Sharpe Ratio: 0.6295739542629956
Average Sharpe Ratio of all generated: 0.41769013603936234
SubSet 74 average Sharpe Ratio: 0.4737515886960216
Average Sharpe Ratio of all generated: 0.41843762207478447
SubSet 75 average Sharpe Ratio: 0.3635227299976354
Average Sharpe Ratio of all generated: 0.41771505770534834
SubSet 76 average Sharpe Ratio: 0.3015802060824008
Average Sharpe Ratio of all generated: 0.4162068128790763
SubSet 77 average Sharpe Ratio: 0.36644780378494485
Average Sharpe Ratio of all generated: 0.41556887686504895
SubSet 78 average Sharpe Ratio: 0.50123337455355
Average Sharpe Ratio of all generated: 0.41665323759528317
SubSet 79 average Sharpe Ratio: 0.19362707232746879
Average Sharpe Ratio of all generated: 0.41386541052943543
SubSet 80 average Sharpe Ratio: 0.3515623457587216
Average Sharpe Ratio of all generated: 0.41309623689029085
SubSet 81 average Sharpe Ratio: 0.4212058872013709
Average Sharpe Ratio of all generated: 0.41319513506481625
SubSet 82 average Sharpe Ratio: 0.3879017687044189
Average Sharpe Ratio of all generated: 0.4128903957110765
SubSet 83 average Sharpe Ratio: 0.36983110842487227
Average Sharpe Ratio of all generated: 0.41237778514814555
SubSet 84 average Sharpe Ratio: 0.2578248069669768
Average Sharpe Ratio of all generated: 0.4105595148166024
SubSet 85 average Sharpe Ratio: 0.14658122462663692
Average Sharpe Ratio of all generated: 0.4074899998143935
SubSet 86 average Sharpe Ratio: 0.5089210029396428
Average Sharpe Ratio of all generated: 0.4086558734135343
SubSet 87 average Sharpe Ratio: 0.6290963485180835
Average Sharpe Ratio of all generated: 0.4111608788124496
SubSet 88 average Sharpe Ratio: 0.40372917771106126
Average Sharpe Ratio of all generated: 0.4110773765528835
SubSet 89 average Sharpe Ratio: 0.37219148938060614
Average Sharpe Ratio of all generated: 0.4106453111398582
SubSet 90 average Sharpe Ratio: 0.48920044749231667
Average Sharpe Ratio of all generated: 0.4115085543964786
SubSet 91 average Sharpe Ratio: 0.48136955070024484
Average Sharpe Ratio of all generated: 0.4122679130519543
SubSet 92 average Sharpe Ratio: 0.42248164709077335
Average Sharpe Ratio of all generated: 0.4123777381491459
SubSet 93 average Sharpe Ratio: 0.47995131841688593
Average Sharpe Ratio of all generated: 0.4130966060243347
SubSet 94 average Sharpe Ratio: 0.4266665487658641
Average Sharpe Ratio of all generated: 0.4132394475268771
SubSet 95 average Sharpe Ratio: 0.2458783835027157
Average Sharpe Ratio of all generated: 0.4114961031099587
SubSet 96 average Sharpe Ratio: 0.5921694597637205
Average Sharpe Ratio of all generated: 0.4133587150342243
SubSet 97 average Sharpe Ratio: 0.23829316741527026
Average Sharpe Ratio of all generated: 0.4115723318952554
SubSet 98 average Sharpe Ratio: 0.5550459365954736
Average Sharpe Ratio of all generated: 0.41302156022556064
SubSet 99 average Sharpe Ratio: 0.44692153394428374
Average Sharpe Ratio of all generated: 0.4133605599627479

古典アルゴリズムによる探索#

次にQUBO行列の準備及び古典なアルゴリズムに必要な関数を実装します。ここで、ペアワイズ相関行列は論文に従い対数リターンで計算を行います。

import heapq
import pandas as pd
import copy

#Attractiveness Coversion
def SRBucket(SR_list):
    Buckets=sorted(SR_list)
    Buckets.reverse()
    GroupedList = list(np.array_split(Buckets,11))
    for i in range(len(SR_list)):
        if   SR_list[i] in GroupedList[0]: SR_list[i]=15
        elif SR_list[i] in GroupedList[1]: SR_list[i]=12
        elif SR_list[i] in GroupedList[2]: SR_list[i]=9
        elif SR_list[i] in GroupedList[3]: SR_list[i]=6
        elif SR_list[i] in GroupedList[4]: SR_list[i]=3
        elif SR_list[i] in GroupedList[5]: SR_list[i]=0
        elif SR_list[i] in GroupedList[6]: SR_list[i]=-3
        elif SR_list[i] in GroupedList[7]: SR_list[i]=-6
        elif SR_list[i] in GroupedList[8]: SR_list[i]=-9
        elif SR_list[i] in GroupedList[9]: SR_list[i]=-12
        elif SR_list[i] in GroupedList[10]: SR_list[i]=-15

#Penalty/Reward Conversion 
def CorrelationBucket(Corr):
    for i in range(len(Corr)):
        for j in range(len(Corr)):
            if Corr[i][j] >= -1.00 and  Corr[i][j] < -0.25: Corr[i][j] = -5
            elif Corr[i][j] >= -0.25 and  Corr[i][j] < -0.15: Corr[i][j] = -3
            elif Corr[i][j] >= -0.15 and  Corr[i][j] < -0.05: Corr[i][j] = -1
            elif Corr[i][j] >= -0.05 and  Corr[i][j] < 0.05: Corr[i][j] = 0
            elif Corr[i][j] >= 0.05 and  Corr[i][j] < 0.15: Corr[i][j] = 1
            elif Corr[i][j] >= 0.15 and  Corr[i][j] < 0.25: Corr[i][j] = 3
            elif Corr[i][j] >= 0.25 and  Corr[i][j] < 1.00: Corr[i][j] = 5

#Ising component for classical algorithms
def hi(SR_list, Corr, i):
    h = 0.5*SR_list[i] + np.sum(Corr[i])
    return h

def jij(Corr, i, j):
    return 1./4.*Corr[i][j]

#Create Pairwise Correlation Matrix
def CreateCorrMat(Chart):
    assets = list()
    for iasset in range(len(Chart)):
        returns = list()
        for month in range(12):
            log_return = np.log(Chart[iasset][month+1]/Chart[iasset][month])
            returns.append(log_return)
        assets.append(returns)
    Chart_pd = pd.DataFrame(assets).T
    pairwise_corr = Chart_pd.corr(method='pearson')
    return pairwise_corr

#Initial state for Greedy Search and Genetic Algorithm
def GenerateRandomSolution(Nassets):
    Solution = np.random.randint(2, size=Nassets)
    for i in range(Nassets):
        Solution[i] = 2*Solution[i] - 1
    return Solution

#得られた解のポートフォリオのSharpe Ratioを計算する
def EvaluateSolution(Solution,Chart):
    selected_assets = list()
    for i in range(len(Solution)):
        if Solution[i] == 1:
            selected_assets.append(Chart[i])
    portfolioChart = np.mean(selected_assets, axis=0)
    portfolioSR = CalculateSharpeRatio(portfolioChart)
    return portfolioSR

#遺伝アルゴリズム、突然変異を導入して子孫を作る
def CreateDescendant(Ancestor, Ndescendants, MaxMutation):
    n = 0
    index_list = range(len(Ancestor))
    Descendants = list()
    while n < Ndescendants:
        Nmutaion = np.random.randint(MaxMutation)
        Place_to_change = np.random.choice(index_list, size=Nmutaion, replace=False)
        Descendant = list()
        for place in Place_to_change:
            Descendant = copy.deepcopy(Ancestor)
            Descendant[place] = Ancestor[place] * -1
            Descendants.append(Descendant)
        n += 1
    return Descendants

#銘柄セットを再生成する
#ここからさっきのステップはこの銘柄セットをずっと使う
Nassets = 48

Chart = CreateAssets(Nassets)
PairwiseCorrMat = CreateCorrMat(Chart)
SR_list = list()

for asset in Chart:
    SR_list.append(CalculateSharpeRatio(asset))

#Bucketの翻訳
SRBucket(SR_list)
CorrelationBucket(PairwiseCorrMat)

#print(PairwiseCorrMat)　#ペアワイズ相関行列の確認

貪欲法による探索#

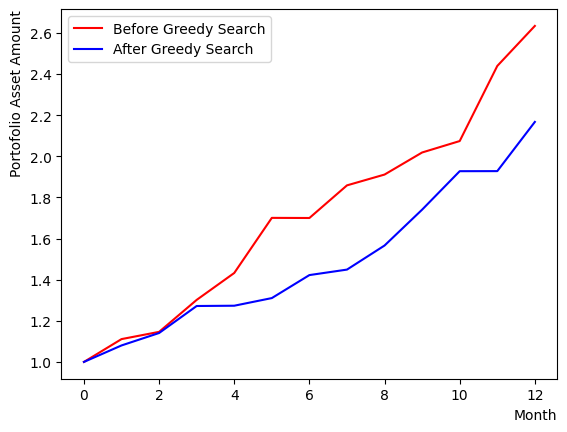
まずは貪欲法アルゴリズムによる探索を行います。ランダムに生成した初期状態から出発し、全体のパフォーマンスに対する影響を見ながら、ポートフォリオのSharpe Ratioを高くできそうな銘柄を選んでいきます。反復を行うことで、ランダムな初期状態からある一定の状態に落ち着くことが観測できます。

実行後、初期状態と貪欲法で得られた状態の比較を行います。このときの比較基準はポートフォリオのSharpe Ratioとします。このチュートリアルでは全銘柄のウエイトが同じというシナリオで計算を行なっているため、選ばれた銘柄の平均的なチャートを得てSharpe Ratioの計算を行っています。

また、一個前のコードブロックを複数回実行して銘柄セットをリセットすると、貪欲法の結果が初期状態よりも悪くなったり、ほぼ変わらなかったりする場合もあることがわかります。また最終的なリターンが初期状態に負けているが、Sharpe Ratioが大きいという最終状態も出現します。それらを比較すると、Sharpe Ratioが大きい場合のポートフォリオはチャートが滑らかで、変動が小さい(リスクが小さい)ことが分かります。

#Greedy Search

#初期状態生成
Solution = GenerateRandomSolution(Nassets)
print("Initial random selection:")
print(Solution, EvaluateSolution(Solution, Chart))
print("")

selected_charts = list()
for i in range(Nassets):
    if Solution[i] == 1:
        selected_charts.append(Chart[i])
portfolioChart = np.mean(selected_charts, axis=0)

#初期状態に基づいてエネルギーの初期化を行う
Energies = list()
for iasset in range(Nassets):
    h = hi(SR_list, PairwiseCorrMat, iasset)
    energyTuple = [-1*abs(h), h , iasset]
    Energies.append(energyTuple)

#貪欲サーチの実行
NGreedyLoop = 10
for i in range(NGreedyLoop):
    heapq.heapify(Energies)

    ntry = 0
    #print(Energies) #エネルギー変化を確認
    while(ntry < len(Energies)):
        x, e, i = heapq.heappop(Energies)
        if e > 0:
            Solution[i] = -1.
        else:
            Solution[i] = 1.
        for ie in Energies:
            n = ie[2]
            ie[1] = ie[1] + Solution[i]*(jij(PairwiseCorrMat, i, n) + jij(PairwiseCorrMat, n, i))
            ie[0] = -ie[1]
        ntry+=1


#貪欲サーチの出力
print("Selection After Greedy Search:")
print(Solution, EvaluateSolution(Solution, Chart))
print("")

selected_charts2 = list()
for i in range(Nassets):
    if Solution[i] == 1:
        selected_charts2.append(Chart[i])
portfolioChart2 = np.mean(selected_charts2, axis=0)

plt.plot(list(range(13)), portfolioChart,color="r",label="Before Greedy Search")
plt.plot(list(range(13)), portfolioChart2,color="b",label="After Greedy Search")
plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()

Initial random selection:
[ 1 -1 -1  1  1  1 -1 -1  1  1  1 -1  1 -1 -1  1  1  1  1  1 -1 -1  1  1
  1  1  1  1  1 -1 -1  1 -1 -1 -1 -1 -1 -1  1 -1  1  1  1 -1 -1 -1 -1  1] 1.1735856604867643

Selection After Greedy Search:
[-1 -1 -1 -1 -1 -1 -1 -1  1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1  1 -1 -1 -1 -1
 -1 -1  1 -1 -1 -1  1 -1 -1 -1  1 -1  1  1  1 -1 -1 -1  1 -1  1  1 -1 -1] 1.1579202630400593

../../../_images/869dab984d2146faea3ca7b7982a4d512c8851f38f1a4921934081a30e25bde3.png

遺伝的アルゴリズム#

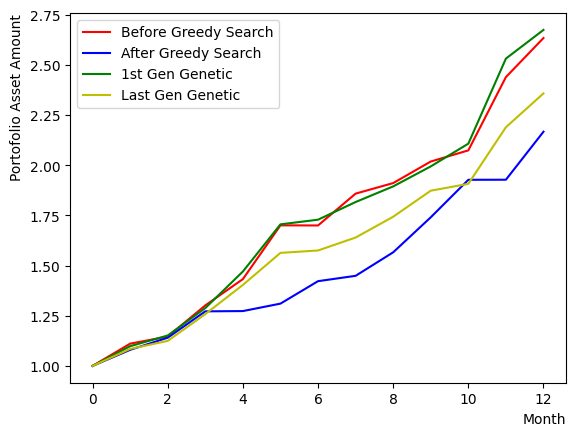
貪欲法のほかに使われた古典アルゴリズムとして、遺伝的アルゴリズムがあります。ランダムに生成した複数のポートフォリオからパフォーマンスが良いものを選択し、その良いポートフォリオをもとにして次の世代のポートフォリオを生成します。次の世代のポートフォリオは、前の世代のポートフォリオにランダムな変更を加える突然変異と、ポートフォリオ間の遺伝子を交換させる操作などから生成されます。ここでは銘柄数が比較的小さいため、突然変異のみを考えて、遺伝子間の交換などは行わないものとします。

結果を比較することで、最後に計算された世代のパフォーマンスは第一世代よりも良くなっていることがわかります。ただし、ここでは試行した世代数が限られているため、パフォーマンスが改善されないまたは改善が小さい場合もあります。しかし、総じて貪欲法よりも安定な出力が得られることも観察できます。

注意：遺伝子の組数や子孫数そして変異の数を増やした場合、計算量の増加により計算が終わらない場合もあります。実行環境に合わせて設定を変更してください。

#Genetic Algorithm
Ngenes = 10 #遺伝子の組数
NGenerations = 5 #世代数
#ランダム初期化
Genes = list()
for i in range(Ngenes):
    gene = GenerateRandomSolution(Nassets)
    geneSR = EvaluateSolution(gene, Chart)
    Genes.append([geneSR, gene])
Genes = sorted(Genes,reverse=True)

#第一世代最優良ポートフォリオ
print("Best Gene 1st generation:")
print(Genes[0][1], EvaluateSolution(Genes[0][1], Chart))
print("")

selected_charts3 = list()
for i in range(Nassets):
    if Genes[0][1][i] == 1:
        selected_charts3.append(Chart[i])
portfolioChart3 = np.mean(selected_charts3, axis=0)


#遺伝的アルゴリズム実行
K_best = 5 #上位抽出遺伝子組数
Ndescendants = 2 #子孫数
MaxMutation = 2 #最大変異数
for iIter in range(NGenerations):
    selected_Genes = Genes[:K_best]
    for gene in selected_Genes:
        Descendants = CreateDescendant(gene[1], Ndescendants, MaxMutation)
        for Descendant in Descendants:
            DescendantSR = EvaluateSolution(Descendant, Chart)
            selected_Genes.append([DescendantSR, Descendant])
    selected_Genes = sorted(selected_Genes, key=lambda x: x[0], reverse=True)
    selected_Genes = copy.deepcopy(selected_Genes[:K_best])

#ラスト世代最優良ポートフォリオ
print("Best Gene last generation:")
print(selected_Genes[0][1], EvaluateSolution(selected_Genes[0][1], Chart))
print("")
selected_charts4 = list()
for i in range(Nassets):
    if selected_Genes[0][1][i] == 1:
        selected_charts4.append(Chart[i])
portfolioChart4 = np.mean(selected_charts4, axis=0)

#比較プロットを作る
plt.plot(list(range(13)), portfolioChart,color="r",label="Before Greedy Search")
plt.plot(list(range(13)), portfolioChart2,color="b",label="After Greedy Search")
plt.plot(list(range(13)), portfolioChart3,color="g",label="1st Gen Genetic")
plt.plot(list(range(13)), portfolioChart4,color="y",label="Last Gen Genetic")
plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()

Best Gene 1st generation:
[-1  1  1 -1 -1  1 -1  1 -1 -1  1  1  1 -1  1  1 -1  1  1 -1 -1 -1 -1  1
  1  1 -1 -1  1 -1  1 -1  1  1 -1  1 -1  1  1  1  1 -1  1  1 -1  1  1 -1] 1.2613442436510724
Best Gene last generation:
[-1 -1  1 -1  1  1  1 -1 -1 -1  1 -1  1  1  1 -1  1 -1  1  1  1 -1 -1  1
  1  1 -1 -1 -1 -1  1 -1  1 -1  1 -1 -1  1  1 -1 -1 -1  1 -1  1 -1 -1  1] 1.3715997785797907

../../../_images/38709507dd4691360d7cc8ea8156a0e925bd1cd7676765163f274e8813ad5b50.png

OpenJijを用いた量子アニーリング手法の実装#

Quantum Annealingによる解法#

Reverse Quantum Annealingでこの最適問題解くために、古典なアルゴリズムで得られたスピン形式の結果をアニーリングが使う形式に変換しましょう。

def ConvertSolutionToQuboState(solution):
    output = list()
    for i in range(len(solution)):
        if solution[i] == 1:
            output.append(1)
        else: output.append(0)
    return output

QA_init_state = ConvertSolutionToQuboState(Solution) #貪欲サーチの結果を初期状態として使う
#QA_init_state = ConvertSolutionToQuboState(selected_Genes[0][1]) #遺伝的アルゴリズムラスト世代の最優良ポートフォリオを初期状態として使う
#QA_init_state = GenerateRandomSolution(Nassets) #ランダムな初期状態を使う
print(QA_init_state)    

[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0]

Forward Annealingの場合#

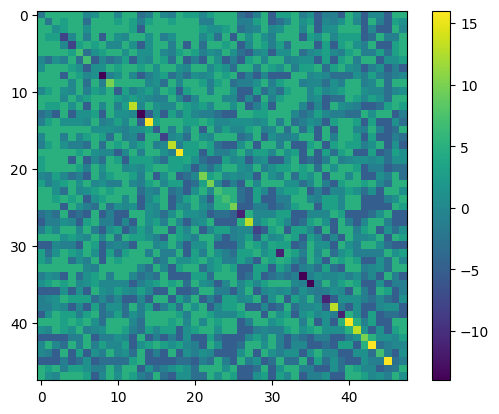
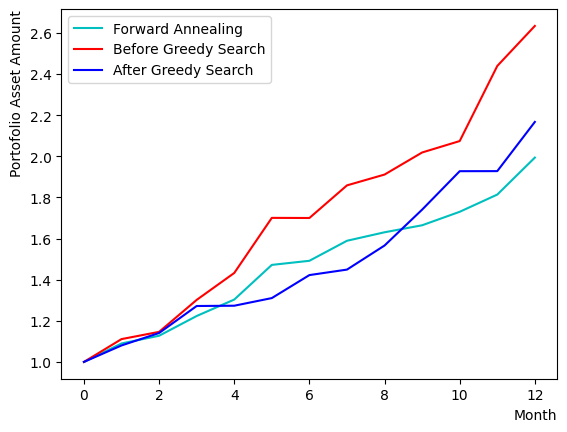
まずはForward Annealingを実行してみましょう。銘柄の魅力度とペアワイズ相関による罰金と賞金の度合を使ってQUBO行列を作ります。以下では量子アニーリングを古典計算機上でシミュレートするSimulated Quantum Annealing (SQA)を用いて計算を行います。最終リターン率の改善は場合によりますが、貪欲法で得られた結果よりも安定したチャートを得られていることがわかります。

from openjij import SQASampler
sampler = SQASampler()

QUBO = np.random.rand(Nassets**2).reshape(Nassets, Nassets)
for i in range(Nassets):
    for j in range(Nassets):
        QUBO[i][j] = PairwiseCorrMat[i][j]
for i in range(Nassets):
    QUBO[i][i] = QUBO[i][i] + SR_list[i]

print(type(QUBO))
import matplotlib.pyplot as plt
plt.imshow(QUBO)
plt.colorbar()
plt.show()

sampleset_FQA = sampler.sample_qubo(QUBO,num_reads=10)
print(sampleset_FQA.record)
print(sampleset_FQA.record[0][0], EvaluateSolution(sampleset_FQA.record[0][0], Chart))
selected_charts = list()
for i in range(Nassets):
    if sampleset_FQA.record[0][0][i]:
        selected_charts.append(Chart[i])
portfolioChart_FQA = np.mean(selected_charts, axis=0)
plt.plot(list(range(13)), portfolioChart_FQA, color="c", label="Forward Annealing")
plt.plot(list(range(13)), portfolioChart,color="r",label="Before Greedy Search")
plt.plot(list(range(13)), portfolioChart2,color="b",label="After Greedy Search")
plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()

<class 'numpy.ndarray'>
[([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)]
[1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 1 1
 1 1 1 0 0 1 0 1 1 1 1] 1.2547352671430967

../../../_images/04aa19afb89397d2c1ff7baedcf6bd5a168a02c7aae2c266285a0f03d2596517.png

../../../_images/cc3df03a919b3ceab8e73fb49e45a17a46d3e3702162d9f0f21df829c39c4565.png

Reverse Quantum Annealing(RQA)の場合#

Reverse Annealingの場合、まずは古典的アルゴリズムから得られた状態を初期状態として入力してからアニーリングを行います。まずはアニーリングのスケジュールの設定です。ここではOpenJijを用いてSQAのハミルトニアンは次のように定めます。

\mathcal{H}_{\mathrm{SQA}}(s) = s\mathcal{H}_{p}-(1-s)\sum_{i}\sigma_{i}^{x}, 0\leq x\leq 1

ここで $\mathcal{H}_{p}$ は最適解を求めたい問題ハミルトニアンで、 $s$ と $1-s$ はそれぞれ参考論文[2]の $B[t]$ と $A[t]$ に対応します。この $s$ は

sample_qubo(QUBO, num_reads=10)

に追加の引数を指定することによって設定できます。初期状態の設定や更新を含めて、先程のsample_qubo部分を

sample_qubo(QUBO, schedule = user_schedule, initial_state = user_initial_state, num_reads=10, reinitialize_state = False)

のように変更すれば良いでしょう。ここのscheduleはアニーリングスケジュールを指しており

user_schedule = [
    [0, 0.1, 4], #s=0, beta=0.1, 4 steps
    [0.5, 1, 3],  #s=0, beta=1, 3 steps
    [1, 10, 3]  #s=1, beta=10, 3 steps
]

のような構造を持ちます。格納されたリストの[0]成分は $s$ の値で、アニーリング時の横磁場の強さを反映しています。[1]成分は逆温度 $\beta$ を表しています。大きければ低い温度を意味し、より基底状態に到達しやすくなります（デフォルトでは $\beta = 5$ で設定されています。）そして最後の[2]成分は量子モンテカルロ法のシミュレーションステップ数を表しており、各スケジュールの長さを調整できます。

initial_stateの引数に代入する初期状態を指定します。reinitialize_stateのオプションをFalseにすると、反復実行において前ステップでのアニーリング出力が次のステップのアニーリング初期状態として代入されます。上述のスクリプト例では、古典アルゴリズムで準備された初期状態から出発し、RQAを10回実行することになります。このオプション引数のデフォルトであるTrueでは、実行するたびに初期状態の再設定を行います。RQAを一回実行し、複数回の結果を比較したい場合はreinitialize_state = Trueにすると良いでしょう。

ではReverse Annealingのスケジュールを作成しましょう。OpenJijのsamplerは指定された $s$ と $\beta$ を指定したMC step数で量子モンテカルロを実行するため、短い定数をつなぎ合わせて $s$ や $\beta$ が少しずつ変化するようなスケジュールを作り、RQAを動作させる必要があります。ここでは $s$ の変化に注目してそれをプロットすると逆さまの台形のスケジュールを確認できます。横軸は量子モンテカルロ法のモンテカルロステップ数を表します。スケジュール作成関数の中身を書き換えれば、そのほかの形のスケジュールを自在に作成することができます。

def ScheduleFunction(x, RQAschedule):
    for step in RQAschedule:
        length = step[2]
        if x - length > 0:
            x = x-length
            continue
        else:
            s = step[0]
            return s


def ConvertScheduleToPlot(RQAschedule):
    TotalLength = np.sum(RQAschedule, axis=0)[2]
    x = np.arange(0, TotalLength+1)
    s = [ScheduleFunction(n, RQAschedule) for n in x]
    plt.plot(x, s ,label="s")
    plt.xlabel("MC step", loc="right")
    plt.ylabel("$s$, progress of quantum annealing", loc="top")
    plt.legend()
    plt.show()

#Create RQA schedule
RQAschedule = []
NReverseStep = 50
NPauseStep = 50
NForwardStep = 50
NMCStep = 20
TargetS = 0.38
ReverseStep = (1.0 - TargetS) / NReverseStep
ForwardStep = (1.0 - TargetS) / NForwardStep
beta = 5.
#Reverse Step
for i in range(NReverseStep):
    step_sche = [1.0-i*ReverseStep, beta, NMCStep]
    RQAschedule.append(step_sche)   

#Pause Step
RQAschedule.append([TargetS, beta, NPauseStep*NMCStep])

#Forward Step
for i in range(NForwardStep):
    step_sche = [TargetS+(i+1)*ForwardStep, beta, NMCStep]
    RQAschedule.append(step_sche)

#Plot Annealing Schedule
ConvertScheduleToPlot(RQAschedule)

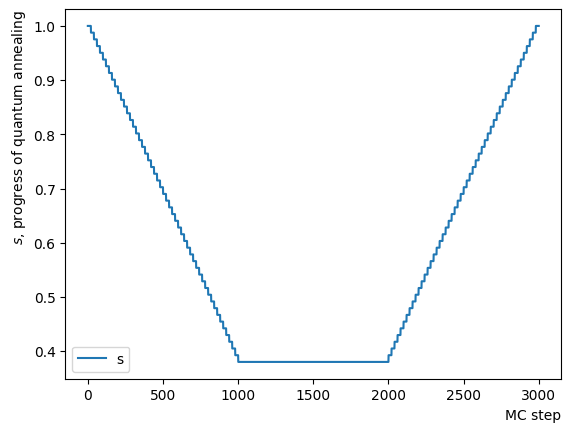
../../../_images/84c6082856d6f3f8b3be2c4d9d09f95a1874ae3fdc21363ef377fcca10ec7107.png

このようにして作成されたスケジュールと初期状態を指定したsample_qubo関数を用いて、RQAを実行しましょう。同時に貪欲法の結果やForward Annealingの結果の比較を行います。結果を見ると、このチュートリアルが行う設定では銘柄セットのサイズ制限によりForward Annealingと同じ最適解にたどり着く場合が多いことがわかります。

#初期状態を準備
init_state = QA_init_state

#Reverse Annealing
sampleset_RQA = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=False)
print(sampleset_RQA.record)

#チャートの比較
selected_charts = list()
for i in range(Nassets):
    if sampleset_RQA.record[0][0][i]:
        selected_charts.append(Chart[i])
portfolioChart_RQA = np.mean(selected_charts, axis=0)
plt.plot(list(range(13)), portfolioChart_FQA, color="c", label="Forward Annealing")
plt.plot(list(range(13)), portfolioChart_RQA, color="m", label="Reverse Annealing")
plt.plot(list(range(13)), portfolioChart,color="r",label="Before Greedy Search")
plt.plot(list(range(13)), portfolioChart2,color="b",label="After Greedy Search")
plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()
#結果の比較
print("Forward Quantum Annealing Result:")
print(sampleset_FQA.record[0][0], EvaluateSolution(sampleset_FQA.record[0][0], Chart))
print("Reverse Quantum Annealing Result:")
print(sampleset_RQA.record[0][0], EvaluateSolution(sampleset_RQA.record[0][0], Chart))

[([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)]
Forward Quantum Annealing Result:
[1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 1 1
 1 1 1 0 0 1 0 1 1 1 1] 1.2547352671430967
Reverse Quantum Annealing Result:
[1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 1 1
 1 1 1 0 0 1 0 1 1 1 1] 1.2547352671430967

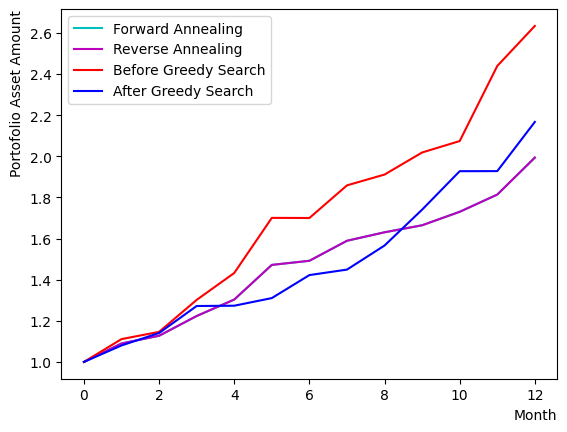
../../../_images/ac46ee133ffb89afb19baabcadaa9657bfa9cbd6e11c37e6e3261e2600475302.png

Reverse Quantum Annealingの確認#

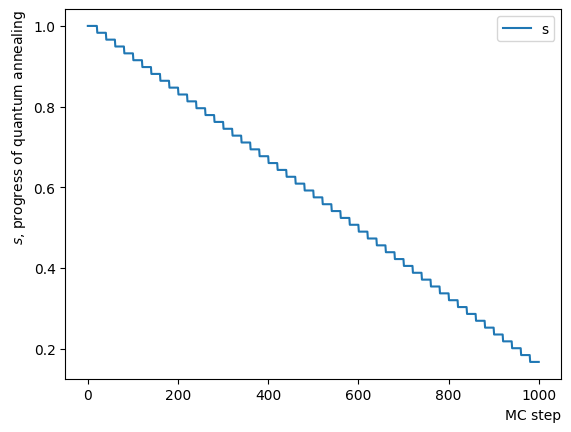
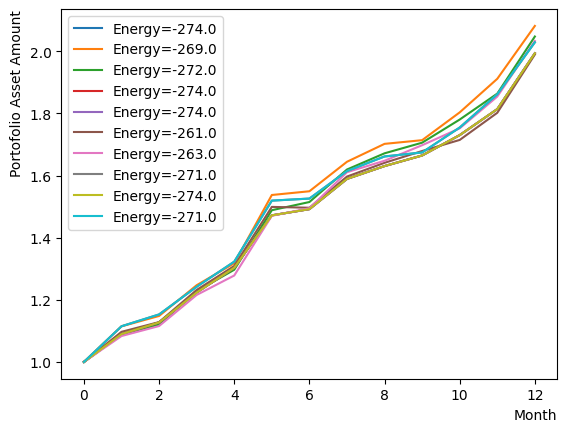
最終出力だけではRQAの振る舞いが分からないため、Phaseを分解してRQAを実行し、その挙動を見てみましょう。まずはReverse Phaseの確認です。同様にアニーリングスケジュールを設定し、スケジュールと初期状態を指定したアニーリングを行います。ここでは分かりやすくするためにReverse Phaseが止まる $s$ の値や逆温度の設定を変更しています。またアニーリングも反復実行するのではなく、毎回同じ初期状態から始まるように設定しました。結果を見ると、Reverse phaseの過程により、既に得られた解からよりエネルギーの高い状態に登っていることがわかります。また実行ごとに異なる状態で留まるため、高いエネルギー準位で解が定まっていない様子も伺えます。

#Create RQA schedule
RQAschedule = []
NReverseStep = 50
TargetS = 0.15 #よりランダムな状態に戻す
ReverseStep = (1.0 - TargetS) / NReverseStep
beta = 5.0
MC_step = 20
#Reverse Step
for i in range(NReverseStep):
    step_sche = [1.0-i*ReverseStep, beta, MC_step]
    RQAschedule.append(step_sche)   

ConvertScheduleToPlot(RQAschedule)
init_state = QA_init_state 
    

sampleset_RQA_Reverse = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
for state in sampleset_RQA_Reverse.record:
    selected_charts = list()
    for i in range(Nassets):
        if state[0][i]:
            selected_charts.append(Chart[i])
    portfolioChart = np.mean(selected_charts, axis=0)
    plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))

plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()
print(sampleset_RQA_Reverse.record)

../../../_images/43b2e946624585c5d7e553d4d67a4dda3fcde7267eeb144b4923bbf942567bbc.png

../../../_images/000cda4a4556aee6659eb424eb644b03e28eca5a54ab384de622f2f35644616c.png

[([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -269., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -272., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -261., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -263., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -271., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -271., 1)]

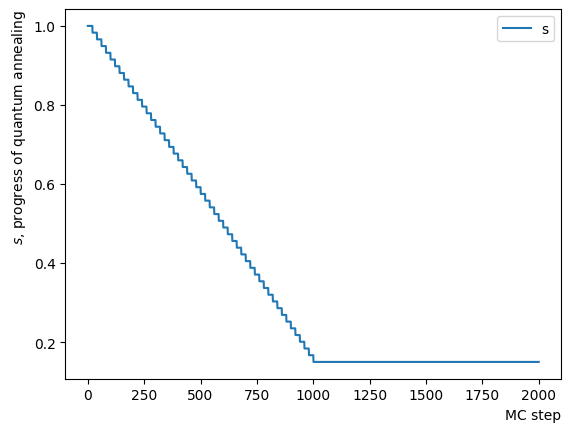
次はPause Phaseの追加を行いましょう。追加後は同様にアニーリングを実行し、その結果を確認します。このPhaseの追加は実装上において上のReverse Phaseの一番最後のステップのMCステップ数を伸ばしたものに等しいため、上のReverseのみのケースと同じようにバラバラの結果となります。

#Create Pause Step
NPauseStep = 50
TargetS = 0.15 #よりランダムな状態に戻す
beta = 1.0 #より高い温度で熱的動きがしやすくようにする
MC_step = 20
step_sche = [TargetS, beta, MC_step*NPauseStep]
RQAschedule.append(step_sche)

#print(RQAschedule)
ConvertScheduleToPlot(RQAschedule)
init_state = QA_init_state 

sampleset_RQA_Reverse_Pause = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
for state in sampleset_RQA_Reverse_Pause.record:
    selected_charts = list()
    for i in range(Nassets):
        if state[0][i]:
            selected_charts.append(Chart[i])
    portfolioChart = np.mean(selected_charts, axis=0)
    plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))

plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()
print(sampleset_RQA_Reverse_Pause.record)

../../../_images/bebf6f5c498e1cda48a6e5b210a1c6d6fd32fcf077adde027b19a9fd278ec814.png

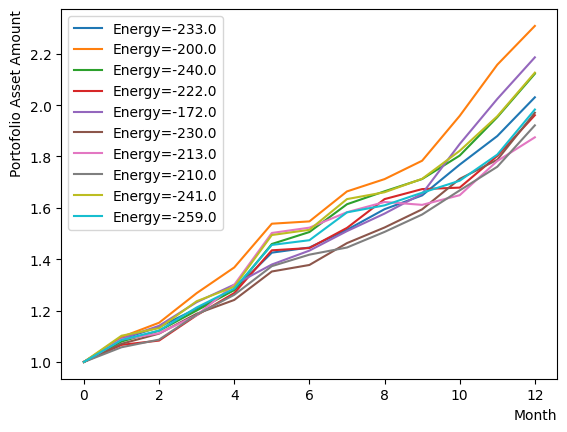
../../../_images/122872d4bbfee0b5caac66f102198c0241d10d7b504ddeeafa267ee72060a836.png

[([0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -233., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1], -200., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1], -240., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1], -222., 1)
 ([0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1], -172., 1)
 ([0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1], -230., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0], -213., 1)
 ([0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1], -210., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1], -241., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -259., 1)]

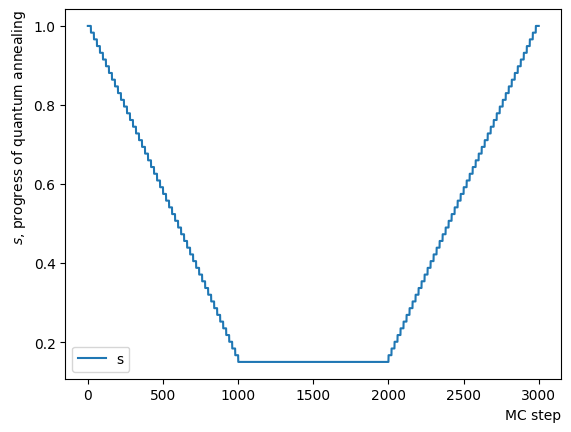
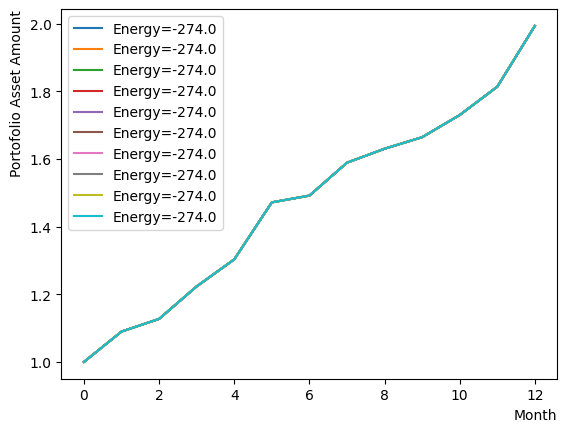
最後にForward Phaseを追加し、アニーリングを実行します。この設定は先程のサンプルよりも少し緩い温度や磁場の条件で行いました。結果として、この銘柄セットで既知の量子アニーリングによる最適解が得られたことがわかります。RQAの節の最初の例と同様に、RQAによって最適解を発見できていることがわかります。

条件が少し緩いため解が収束せず、エネルギーが近い複数のsub-optimalの解の存在を確認することができます。それらの解の中には、場合によりForwardで得られた最適解よりも最終的なリターンが良く、形も比較的に滑らかなポートフォリオの存在も確認できます。そのポートフォリオの詳細を見ると、その大きなリターンは上昇率が大きい特定の銘柄によるもので、逆相関を持つ変動率が比較的に小さい銘柄と組み合わせて実現されたものだと分かります。実際の投資においてはそのようなポートフォリオが好ましいかもしれませんが、このチュートリアルが設定した「Shape Ratioがとにかく最大になる」条件では、相対的に小さいポートフォリSharpe Ratioが実現されたことから、量子アニーリングによって最適ではない解と判断されています。

#Create Forward Step
NForwardStep = 50
TargetS = 0.15 #よりランダムな状態に戻す
ForwardStep = (1.0 - TargetS) / NForwardStep
beta = 5.0 #より高い温度で熱的動きがしやすくようにする
MC_step = 20

#Forward Step
for i in range(NForwardStep):
    step_sche = [TargetS+(i+1)*ForwardStep, beta, MC_step]
    RQAschedule.append(step_sche)

ConvertScheduleToPlot(RQAschedule)
init_state = QA_init_state 

sampleset_RQA_Reverse_Pause_Forward = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
for state in sampleset_RQA_Reverse_Pause_Forward.record:
    selected_charts = list()
    for i in range(Nassets):
        if state[0][i]:
            selected_charts.append(Chart[i])
    portfolioChart = np.mean(selected_charts, axis=0)
    plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))

plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()
print(sampleset_RQA_Reverse_Pause_Forward.record)

../../../_images/0aa33a43ff6508838091a5934766eac3047663ebebc021c1097ce686f0e4552e.png

../../../_images/1047a996769c14c5efd8392af09028087b6488ee7e29b7c7c3c232c63326f3e1.png

[([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)
 ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1], -274., 1)]

RQAスケジュールを指定するときのパラメータ探索#

Phaseを分けてReverse Quantum Annealingの様子を確認するところで、スケジュールの設定に指定した $s$ , $\beta$ 、そして量子モンテカルロ法のステップ数によって結果が変化することが分かりました。このことから、Reverse Annealingでパフォーマンスを良くするには適切な値を設定する必要があるとわかります。

Reverse Phaseの場合#

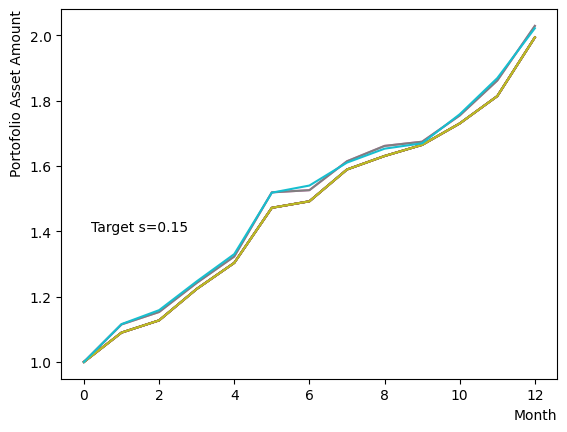
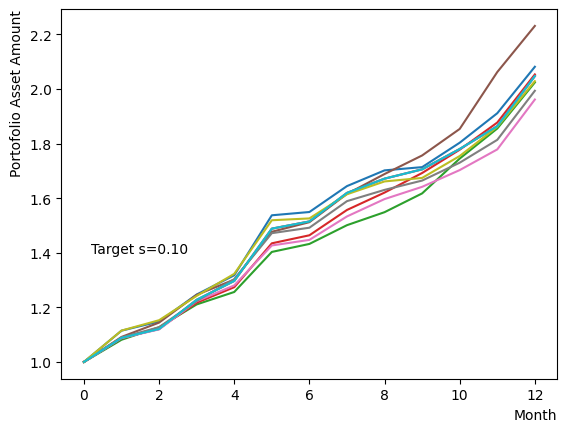
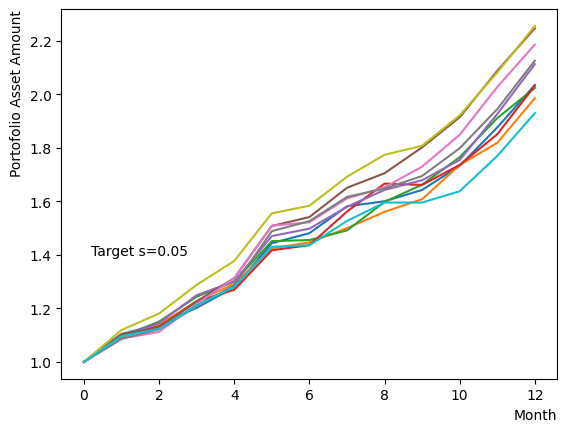
まずはそれらがReverse Phaseに対する影響を見てみましょう。まずは量子アニーリングの度合を表す $s$ の影響から解析します。これは横磁場をどの程度強く戻すのかを表す量であり、最初のアニーリングで辿り着いた局所解の周りにあるポテンシャル障壁を越えて状態がばらけるようにするために、適切な強さ（ $s$ の適切な小ささ）を設定しなければなりません。このノートの結果では $s=0.20$ まではReverse Phaseの終状態のばらつきがあっても不定にはならず、 $s \leq 0.20$ では熱的揺らぎが支配的になり、ばらつきが大きくなる様子が分かります。よって $s \sim 0.2$ の近傍をさらに細かくスキャンすれば、最適の $s$ 値が得られると予想されます。

for TargetS in reversed(np.arange(0.05, 1.0, 0.05)):
    #Create RQA schedule
    RQAschedule = []
    NReverseStep = 50
    ReverseStep = (1.0 - TargetS) / NReverseStep
    beta = 5.0
    MC_step = 20
    #Reverse Step
    #for i in range(NReverseStep):
    for i in range(NReverseStep):
        step_sche = [1.0-i*ReverseStep, beta, MC_step]
        RQAschedule.append(step_sche)   

    init_state = QA_init_state 


    sampleset_RQA_Reverse = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
    for state in sampleset_RQA_Reverse.record:
        selected_charts = list()
        for i in range(Nassets):
            if state[0][i]:
                selected_charts.append(Chart[i])
        portfolioChart = np.mean(selected_charts, axis=0)
        plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))
    
    plt.xlabel("Month", loc="right")
    plt.ylabel("Portofolio Asset Amount", loc="top")
    plt.text(0.2,1.4, "Target s="+'{:.2f}'.format(TargetS))
    plt.show()

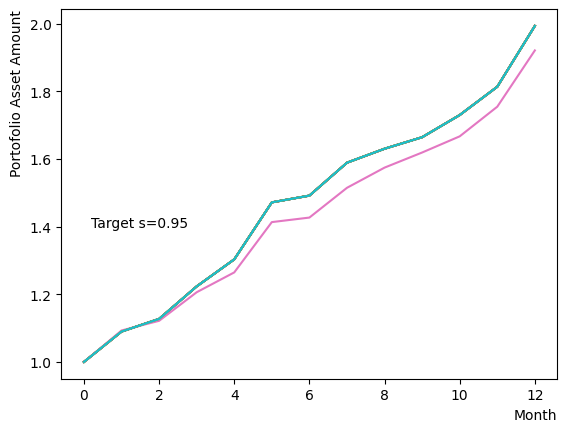
../../../_images/c8f54b23168b06d6a608832557178819d82e1218d311a51c9f11af47b1e46d4a.png

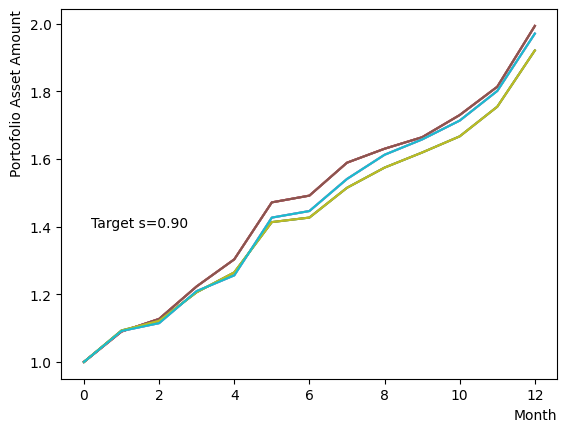
../../../_images/d1c467918f64f3674b45d69d7e6dcc5f71f98c6fda44947adb006867142fee82.png

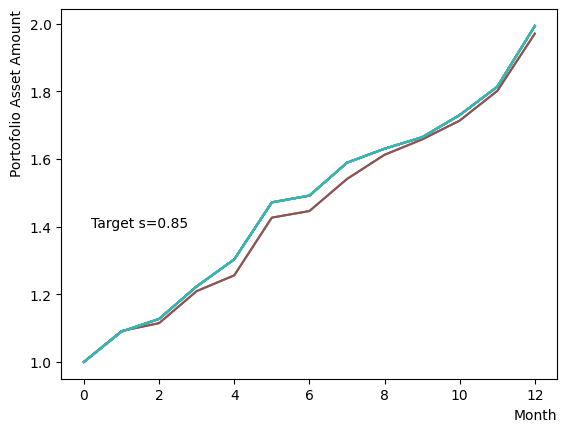
../../../_images/c5dd0a1d38b72f29c5efe07ce604a525878572136cb6174a080deef71e914553.png

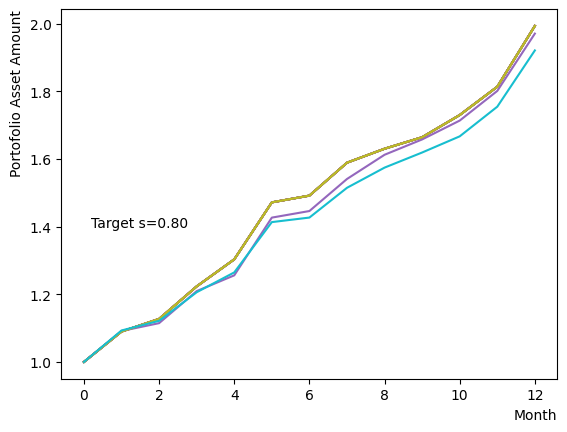
../../../_images/82af922a1dea67e57c347ad388e7d561f216e759fc7070084f15456bf874e351.png

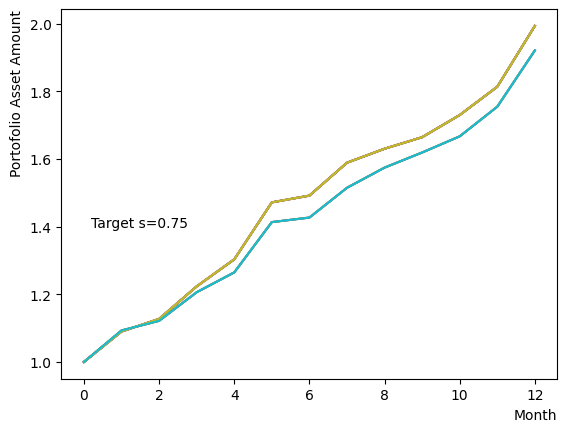
../../../_images/e93348e977a30067e52a469757be4e73d40eefc7be20bb32482cceb944405248.png

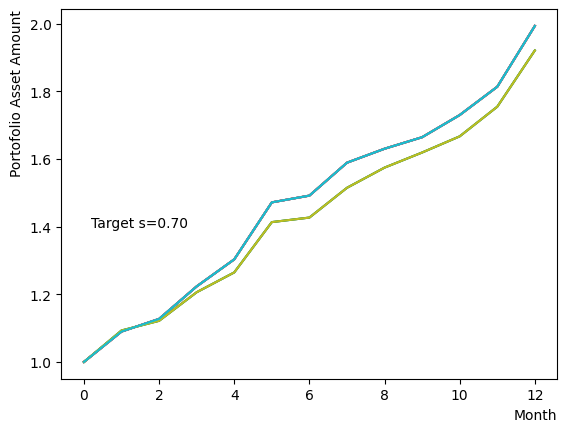
../../../_images/ca36f1c0b802cf2a2ac9abcb46b6596ede67e48f1542e56f96b15a7c9e58babc.png

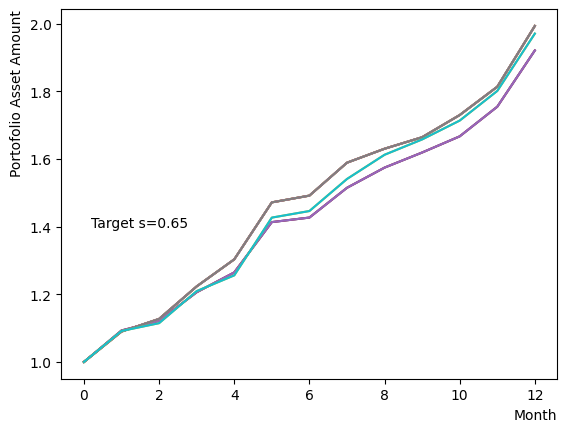
../../../_images/8cabe8296ee56325b0323ff0724741989c60131f1e82e2754c8746064df20c21.png

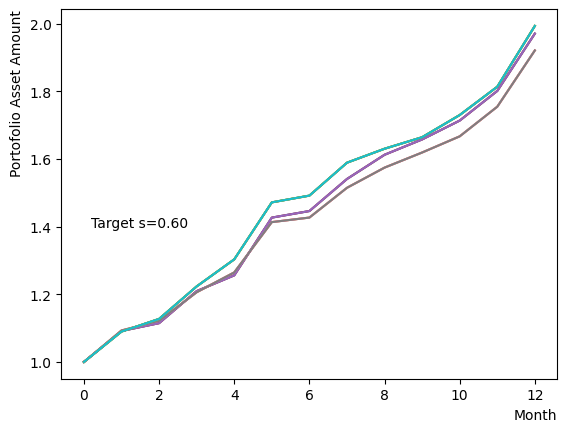
../../../_images/7e2f492dac753aeab69f8ed458243d95c550265e7d9dfa31fb9e9c75d54e0f2e.png

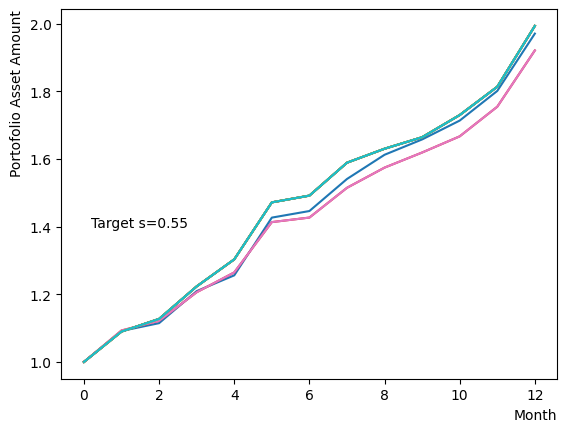
../../../_images/63eb9af8963cb1b36c717b0a2f4d267accb3f2ca8e5009bf32935af4137e6c63.png

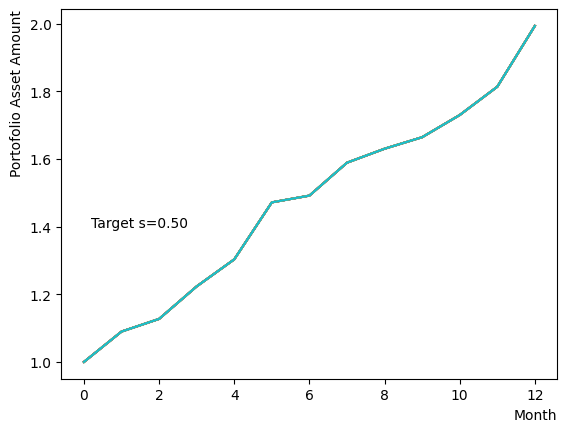
../../../_images/b1ad2b2d45f58f287e4e827f29bf6aaece15730f672807ccfea6869f500eece4.png

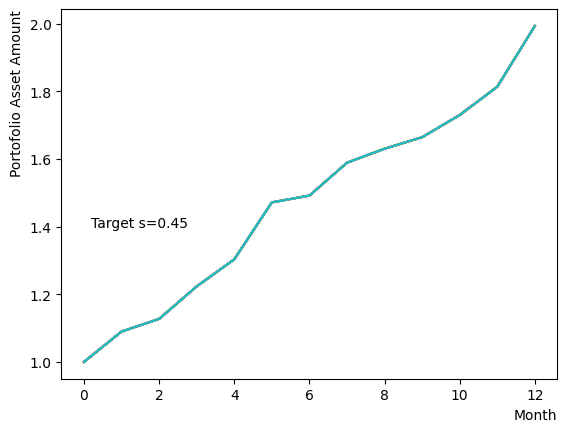
../../../_images/898efe5634531ece0cc1e1fb114062ade89de9fa366362255e59f715a82739a5.png

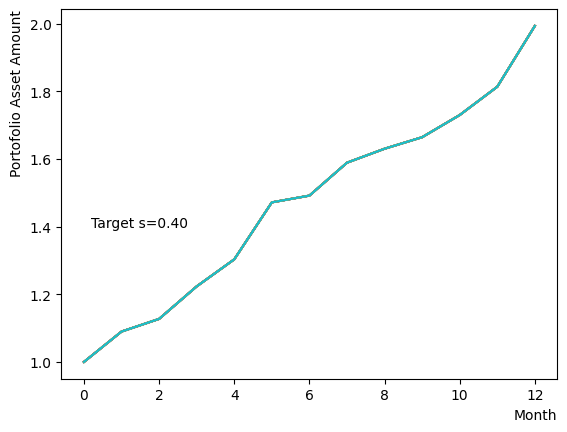
../../../_images/170d6a5ba0ada9645873ba914bfd504216ee6bedabab772d65f91cf7d5190b0c.png

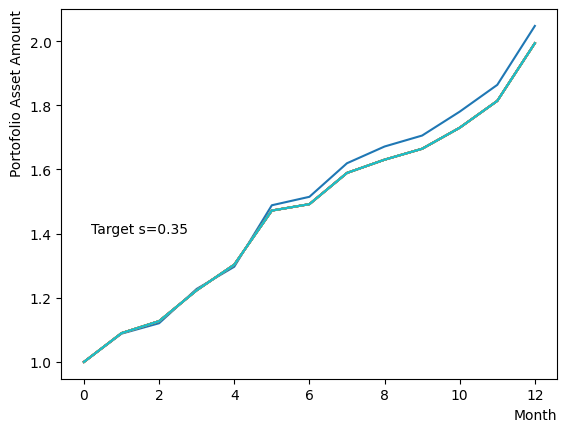
../../../_images/273dfcd1937a4da344c1991dfe9341687719ad714e4ffd5579d9bdca96cba4db.png

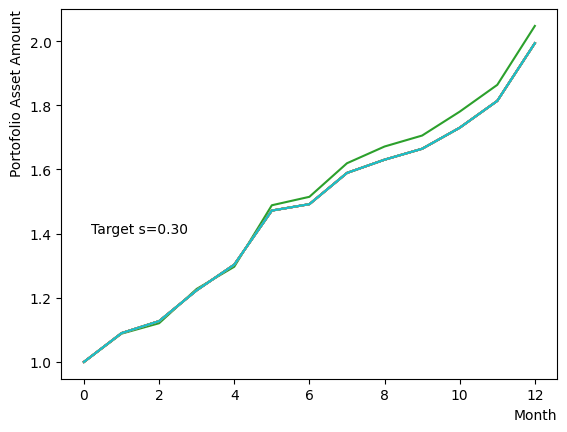
../../../_images/63a35a6ccb5f4da8e33fe958d3416973c3d32a39176b2022c94c3c89294d341d.png

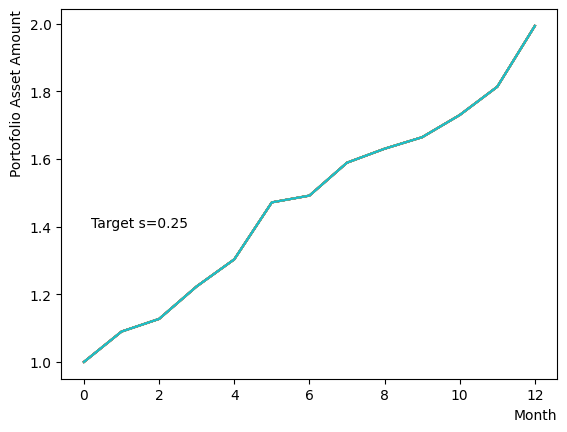
../../../_images/946b9ee27df425b5c6b58d6d34ec1effe542696bbae9ce5a049518d09ccc8fcb.png

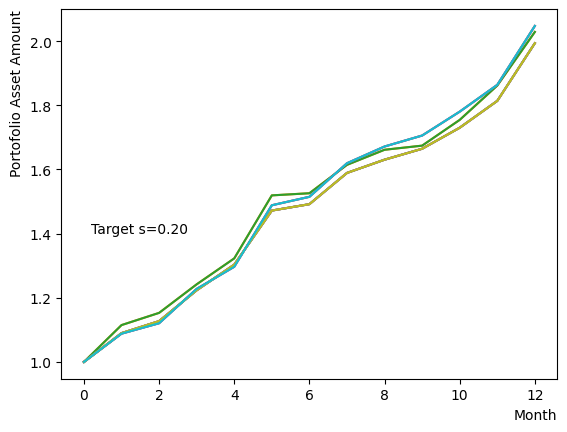
../../../_images/f05cacad2f9d8fb2686a502dc31f613e676e655bd14ac72fc39c90a0beb767cf.png

../../../_images/66c3144a9f007936efdfb28573791b7ee844a4f317d4cb18a30c21cfa9ddbb9c.png

../../../_images/06bc8d02fadd4543e81022eded33273bd5bb18e29c3474009ef99d01b51d58ec.png

../../../_images/eeff7a866ff415c9ddda06040a742cb58b1b7e0fcd9ec7562ad62554cc55f634.png

次に $\beta$ による影響を調べてみましょう。 $\beta = \frac{1}{k_{\mathrm{B}}T}$ は逆温度を表しており、 $\beta$ が大きければ大きいほど系がより低温であることを意味します。 $\beta$ が大きいほど全体としては状態がより基底状態に落ちやすく、より「Annealed」な状態に近い振る舞いをします。言い換えると横磁場が一定の場合、 $\beta$ が大きくなると横磁場が効きにくくなり、実効的には大きい $s$ に近い振る舞いとなります。OpenJijにおいてその影響の詳細を知りたい方はこのQiita記事を参照すると良いでしょう。

また、その影響はQUBO行列に存在するエネルギーの典型的なスケール付近で変わることがわかっています。このチュートリアルの場合、QUBOに入っている典型な値の絶対値は大体 $5$ 程度で収まるため、 $\beta=5.0$ 程度で変化が起こると予想されます。

plt.hist((QUBO).flatten())
plt.xlabel("Values in QUBO", loc="right")
plt.ylabel("Number of entries", loc="top")

Text(0, 1, 'Number of entries')

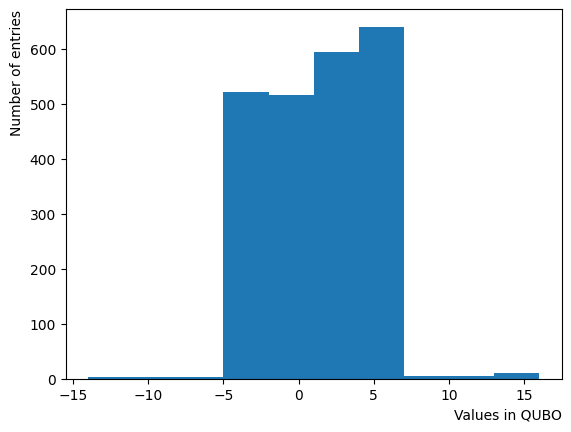
../../../_images/81f32c1ea973c17ea5f5a403fec9b8b9d36d1c65525f9372543c73f2ffc43a97.png

対数的な $\beta$ 配列を用意し、 $s$ 以外の量は固定してReverse Phaseを行います。予想通り $\beta=5$ あたりで終状態のばらつきが小さくなり、それよりも大きい $\beta$ だと数少ない状態に収束してしまう様子がわかります。

for beta in [0.1,0.5,1.0,2.5,5.0,10.0,20.0,50.0]:
    #Create RQA schedule
    RQAschedule = []
    NReverseStep = 50
    TargetS = 0.18
    ReverseStep = (1.0 - TargetS) / NReverseStep
    MC_step = 20
    #Reverse Step
    #for i in range(NReverseStep):
    for i in range(NReverseStep):
        step_sche = [1.0-i*ReverseStep, beta, MC_step]
        RQAschedule.append(step_sche)   

    init_state = QA_init_state 


    sampleset_RQA_Reverse = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
    for state in sampleset_RQA_Reverse.record:
        selected_charts = list()
        for i in range(Nassets):
            if state[0][i]:
                selected_charts.append(Chart[i])
        portfolioChart = np.mean(selected_charts, axis=0)
        plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))
    
    plt.xlabel("Month", loc="right")
    plt.ylabel("Portofolio Asset Amount", loc="top")
    plt.text(0.2,1.8, "beta ="+'{:.2f}'.format(beta))
    plt.show()

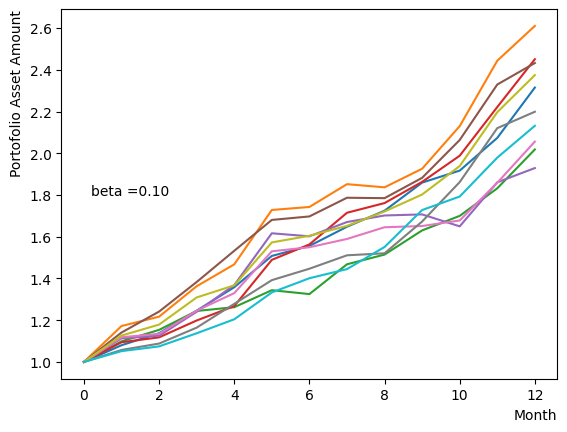
../../../_images/abb10520566efc9be793b734b80f73ef643a6ec758bab511af812447263294fd.png

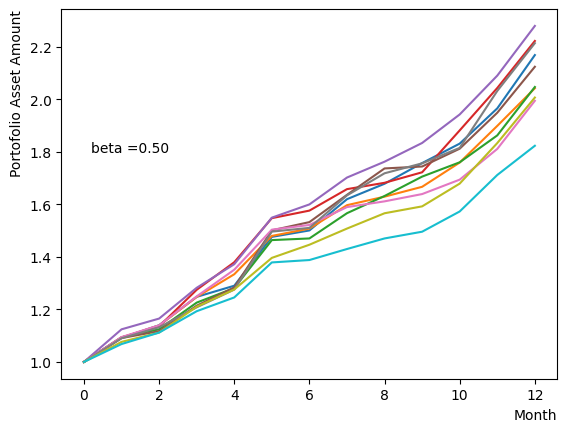
../../../_images/94657b68790648b12bf14d52377776e3f701af5907393401eb574299f09cb402.png

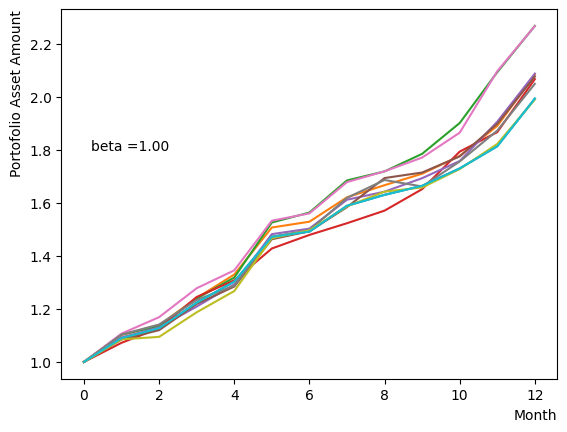
../../../_images/c0cc382477c77f2d8dc82d9ea2c7fdd67a7657598b596467e26e378d75633c20.png

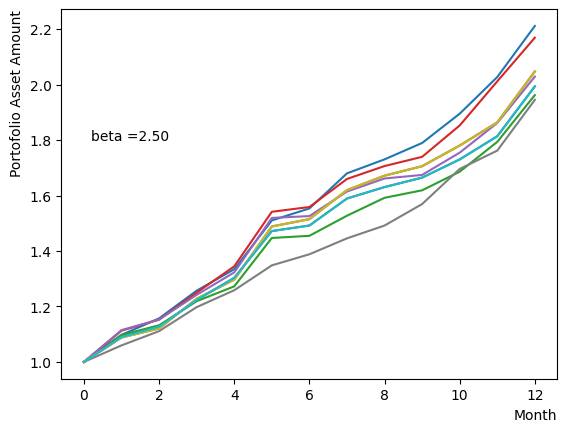
../../../_images/cb30bf9cf60b18138bf6c83377ca045a3ec24858c2847d5c6018118c60ba7ec2.png

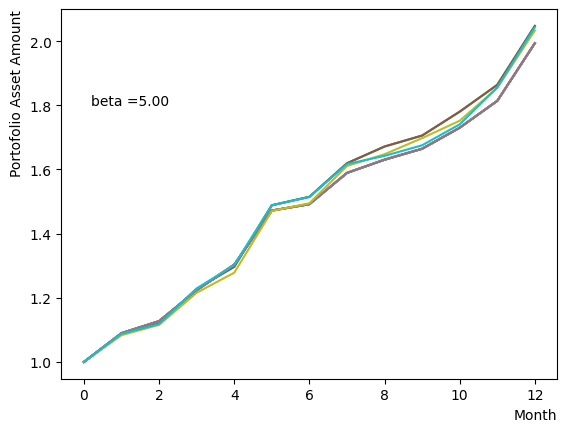
../../../_images/97d5bd2584869a3676ff9fe595fc92968f93cfc04aa480283259fddf94458b72.png

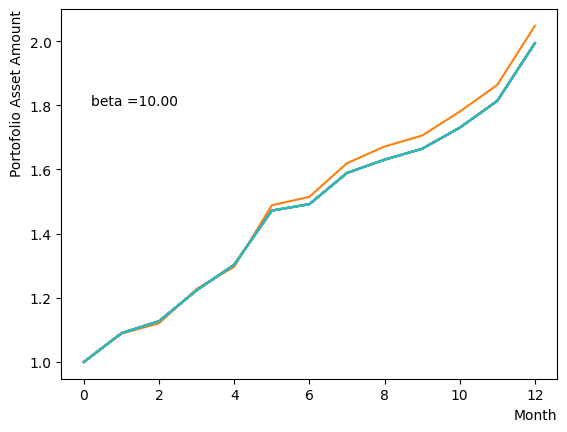
../../../_images/526824c683187b2a99d5d1486d5bc695a6c3ea3692db39c5f2d326a5d9c8a13a.png

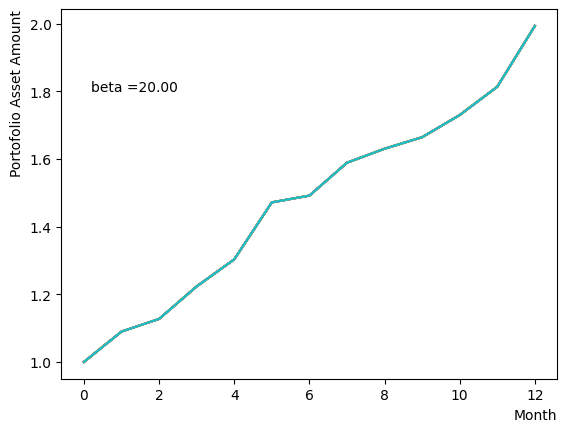
../../../_images/4e6c05be9faa8a9e613620168e720d7ae286540bc6de5dd527f6f570bb8e6f69.png

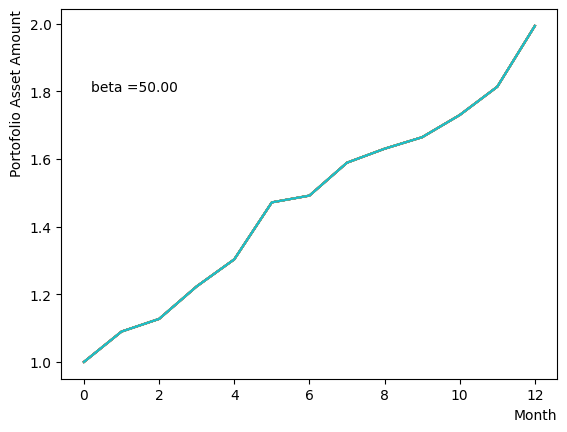
../../../_images/1aeaead069b38bb5420f374a18fbe63119251cd27f0ced09764d7fe3f86553d7.png

そしてスケジュール分割の影響を調べましょう。ここでは階段関数のような極端的な場合から、細かく分割して緩やかな変化にする場合まで調査を行いました。結果から分かるように、分割数が少ない場合には状態があまり変化せず、逆に分割数を増やすとばらつきが見えてきます。また、大きく増やしても計算時間が長くなるだけで、結果の違いが小さいこともも分かります。このチュートリアルが取り扱うポートフォリオ最適化問題の場合は $50$ 程度の設定で問題ないこともわかります。

for NReverseStep in [1,2,5,10,15,20,50,100,500,1000]:
    #Create RQA schedule
    RQAschedule = []
    TargetS = 0.18
    ReverseStep = (1.0 - TargetS) / NReverseStep
    beta = 5.0
    MC_step = 20
    #Reverse Step
    #for i in range(NReverseStep):
    for i in range(NReverseStep):
        step_sche = [1.0-i*ReverseStep, beta, MC_step]
        RQAschedule.append(step_sche)   

    init_state = QA_init_state 


    sampleset_RQA_Reverse = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
    for state in sampleset_RQA_Reverse.record:
        selected_charts = list()
        for i in range(Nassets):
            if state[0][i]:
                selected_charts.append(Chart[i])
        portfolioChart = np.mean(selected_charts, axis=0)
        plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))
    plt.xlabel("Month", loc="right")
    plt.ylabel("Portofolio Asset Amount", loc="top")
    plt.text(0.2,1.8, "NReverseStep ="+'{:.2f}'.format(NReverseStep))
    plt.show()

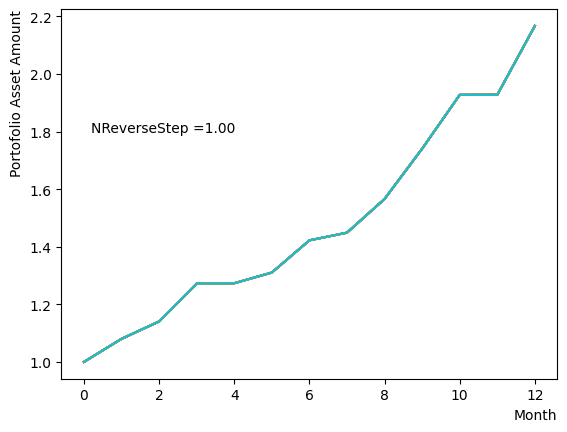
../../../_images/866601a3f952903fe0279c0aa4fb58b72755c82bc6c0b96d995f742e3aaa945e.png

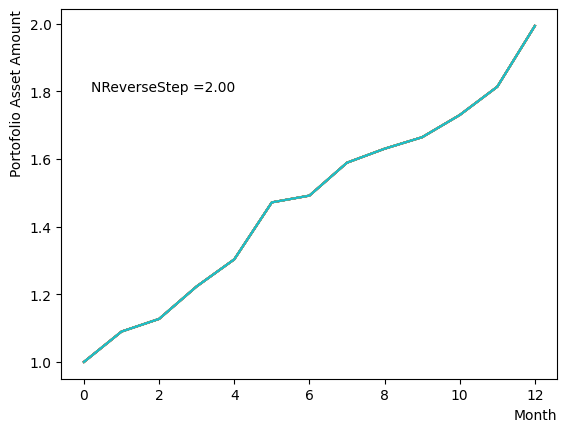
../../../_images/105c94524b3b38b884fe654ca1fa895acd4bff63beb495a5a7eb94b20dee0fda.png

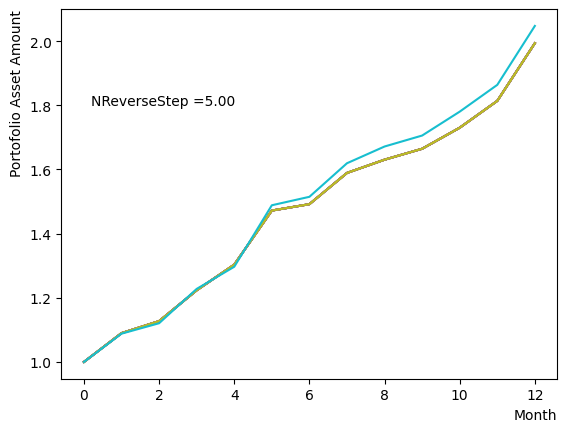
../../../_images/4c932cabce9264e1b3d6e6c10b6ffd6668e60be5fdc0861fa5aed49efb66e01e.png

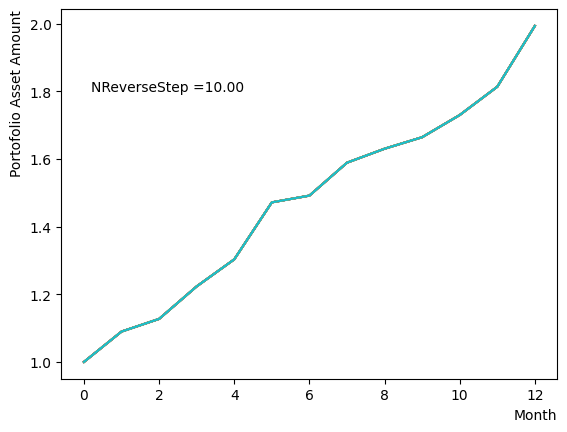
../../../_images/5260148aaae95574ad131f1791cc02f5ef0d160a18021b504e412e2d2cd6726e.png

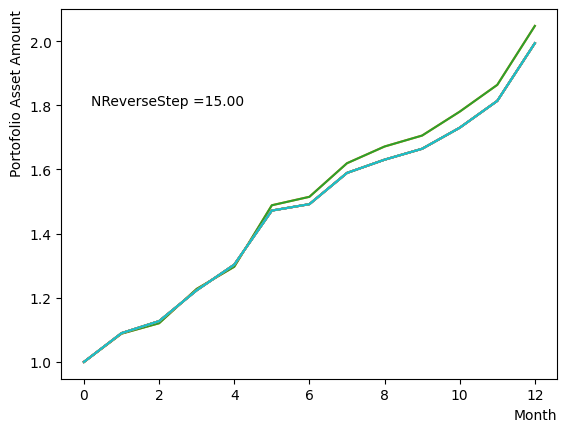
../../../_images/b289713da2205d6c154b4928837ea60e28ece6b40f2fd1f80725018edd947c76.png

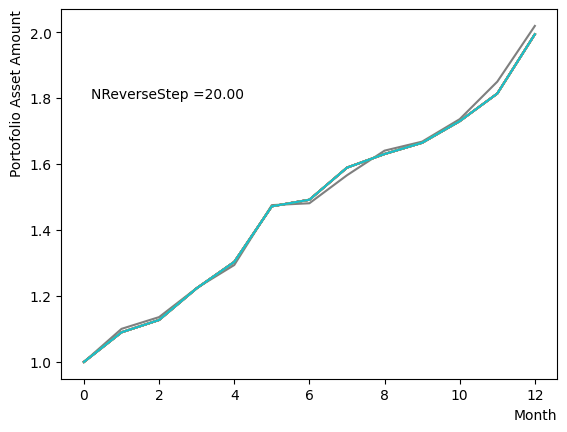
../../../_images/cc69bda444c01240c7f7800b20428e30bc3515e65f7895341d3dc8aa1332d28d.png

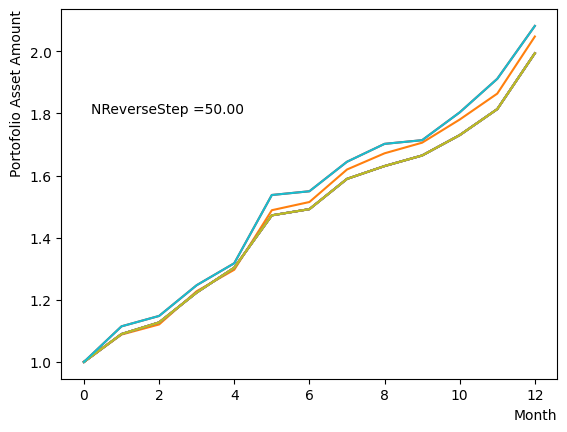
../../../_images/39233ceb1aad4b16b7c148d061596efd38d5508ce2d6ebc91752014f13155dfd.png

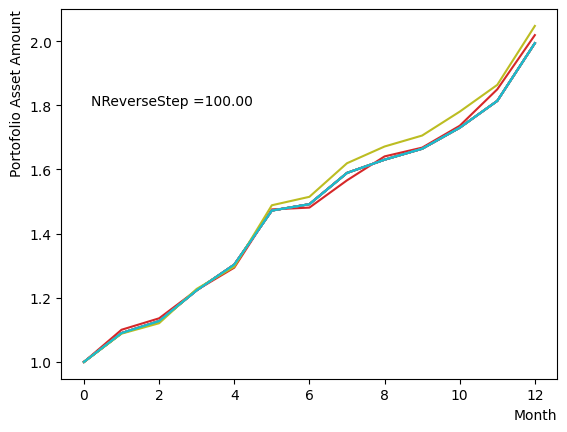
../../../_images/04769bb66094193ffc86206a07de83cdbe6b2c3b28ea16d9883744e22d6c6556.png

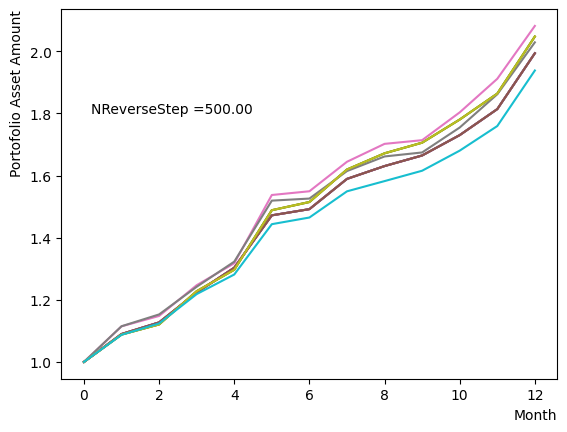
../../../_images/edfa2ecac598602cc5a5e38a972405cf74442f66f9b42681060c69a02809373e.png

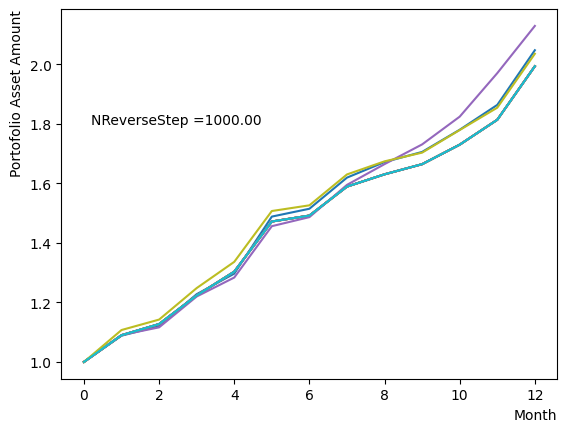
../../../_images/3ec810edc86d952b7a51f050fd15d07d0b95ada2d28741dc62dcf893c209afba.png

またMC stepsに関しては、(分割数)×(MC steps)が極端に少ない場合でなければ、最終の結果にはほぼ影響がないことが分かりました。SQASampler()でデフォルト設定の場合では、目安として $1000$ 程度で問題なく動作するはずです。

Pause Phaseの場合#

既に説明したように、Pause PhaseはReverse Phaseの最後のステップを延長させたものであるため、アニーリング全体の $s$ と $\beta$ を変化させたところでReverse Phaseと同じようなふるまいをします。また、Pause phaseのステップ数はどのぐらい最後のステップを伸ばすのかと言う意味にに等しいため、変更してもほぼReverse Phaseの状態を保持したままであり、影響は少ないと予想されます。

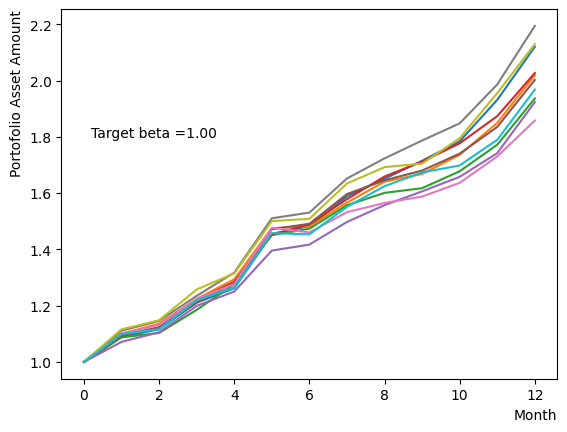
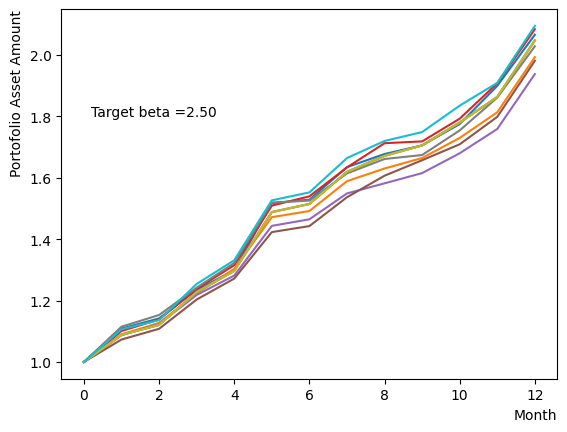
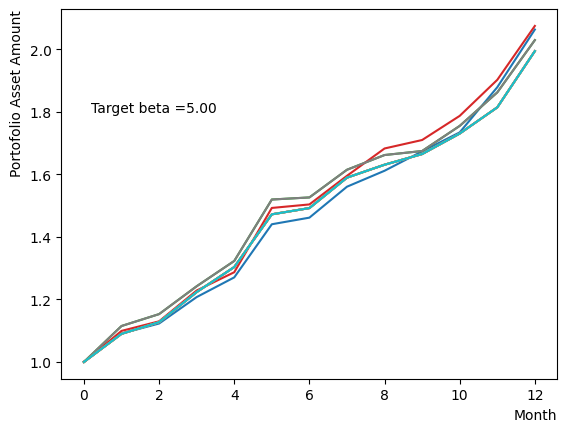
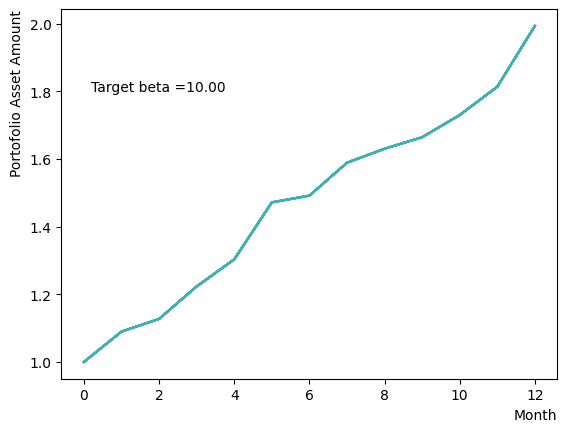
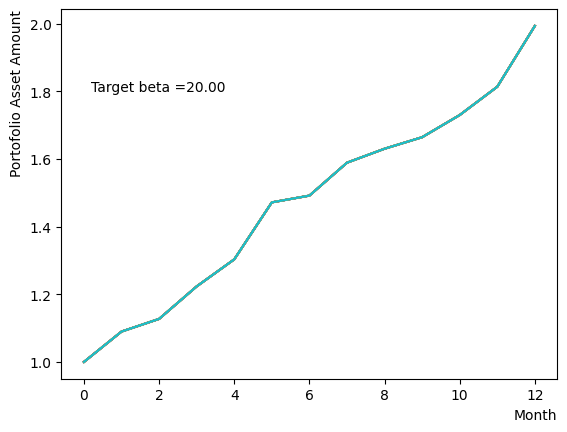
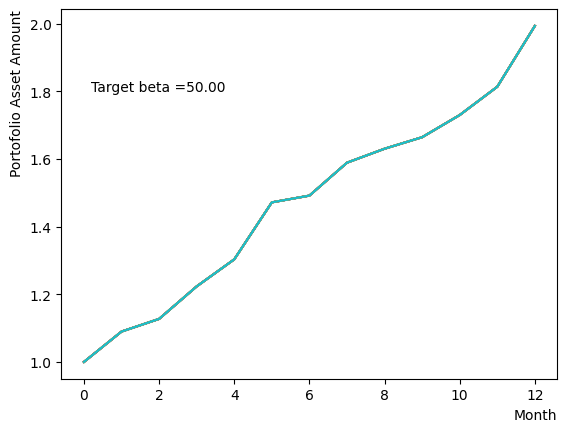
ただし、Pause Phaseだけ $\beta$ を変化させることは量子アニーリングが不完全な状態で古典的なアニーリングを行うことに近い行動です。ここでは $\beta=5.0$ から緩やかに目標とした $\beta$ に向かって系の温度を変化させた場合の影響を調べましょう。Reverse Phaseで異なる $\beta$ でアニーリングを行った場合の終状態に近い結果を得ることができます。

for beta in [0.1,0.5,1.0,2.5,5.0,10.0,20.0,50.0]:
    #Create RQA schedule
    RQAschedule = []
    NReverseStep = 50
    TargetS = 0.18
    ReverseStep = (1.0 - TargetS) / NReverseStep
    MC_step = 20
    #Reverse Step
    #for i in range(NReverseStep):
    for i in range(NReverseStep):
        step_sche = [1.0-i*ReverseStep, 5.0, MC_step]
        RQAschedule.append(step_sche) 
    
    #Pause Phase
    NPauseStep = 50
    betaStep = (5.0-beta) / NPauseStep
    for i in range(NReverseStep):
        step_sche = [TargetS, 5.0-i*betaStep, MC_step]
        RQAschedule.append(step_sche) 

    init_state = QA_init_state 


    sampleset_RQA_Reverse_Pause = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
    for state in sampleset_RQA_Reverse_Pause.record:
        selected_charts = list()
        for i in range(Nassets):
            if state[0][i]:
                selected_charts.append(Chart[i])
        portfolioChart = np.mean(selected_charts, axis=0)
        plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))
    
    plt.xlabel("Month", loc="right")
    plt.ylabel("Portofolio Asset Amount", loc="top")
    plt.text(0.2,1.8, "Target beta ="+'{:.2f}'.format(beta))
    plt.show()

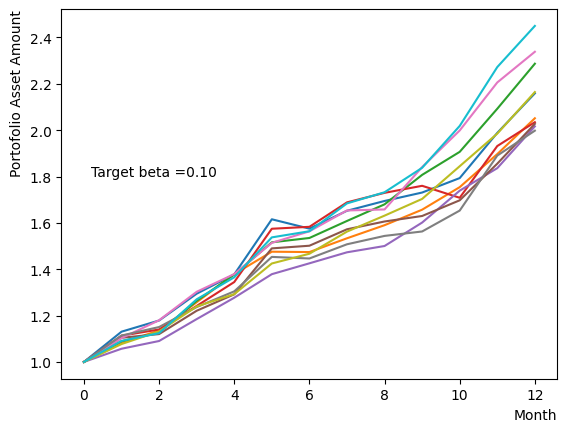
../../../_images/8c1d649987fb5d6dde8b81de8c5550747cbd24353fb2169537e506e550513589.png

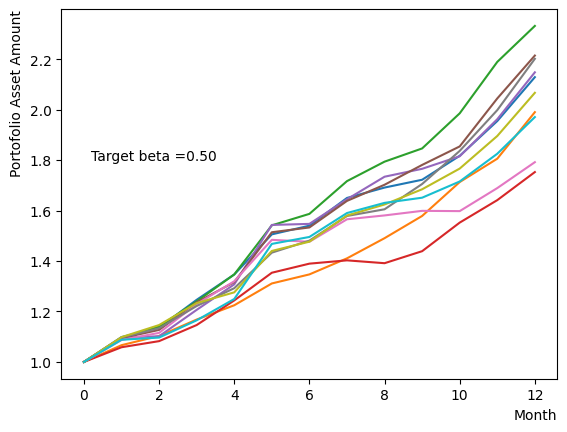
../../../_images/000ba04611243bb055108fbf5361a447687e6d88e3514883a1439adaa548c8ff.png

../../../_images/628052ee4092ac430561ce479863cec19368e5732228a2eb51f45c5aa8ce7205.png

../../../_images/d2fcbff8d2021864124ecb123120cbeb7f6c9fed223915ddfe01a54d557d222a.png

../../../_images/0d2f48c28119405a3741e349b6663460180f8b31551a0d99d0f332efd23923b3.png

../../../_images/8399efd6d3dd4275919227370ff5ba9ba7450d4c459a07eb9f3dad64ea50c35a.png

../../../_images/f2921190147f816f3beae1379f54ad055c58a52044aad4f338d7bcb70807e861.png

../../../_images/535809a1e0d9af58cec286dd844600ee5ab3361d759bae74d49e9973c4d809ae.png

Forward Phaseの場合#

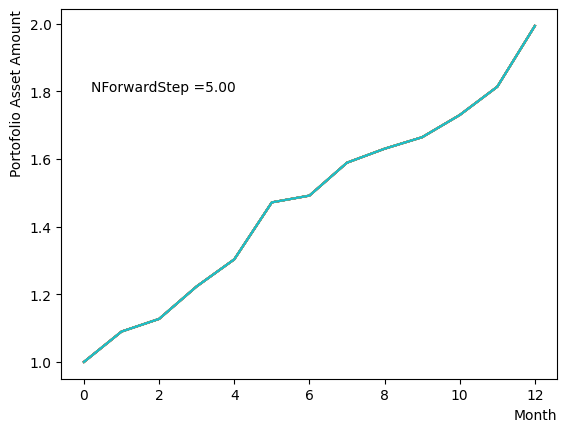
Forwar PhaseはReverse PhaseとPause Phaseを通して得られた状態から普通の量子アニーリングを行うフェーズです。このとき考えるぺきパラメータの条件は、通常のアニーリングが正しく動作するために必要な条件と基本的に同じです。Reverse PhaseとPause Phaseと同じ方法で $\beta$ と分割したステップ数のスキャンを行った結果、比較的小さい分割数と $\beta$ でも結果がちゃんと最適解に収束することが分かりました。

以下にコード例を示します。Reverse PhaseとPause Phaseにおいては、これまでの調査で得られた設定を用いており、Forward Phaseだけ粗い分解と小さい $\beta$ でアニーリングを行っています。

#Create RQA schedule
RQAschedule = []
NReverseStep = 50
TargetS = 0.18
ReverseStep = (1.0 - TargetS) / NReverseStep
MC_step = 20
#Reverse Step
#for i in range(NReverseStep):
for i in range(NReverseStep):
    step_sche = [1.0-i*ReverseStep, 5.0, MC_step]
    RQAschedule.append(step_sche) 
    
#Pause Phase
NPauseStep = 50
step_sche = [TargetS, 5.0, MC_step*NPauseStep]
RQAschedule.append(step_sche) 

#Forward Phase
NForwardStep = 5
ForwardStep = (1.0 - TargetS) / NForwardStep
for i in range(NForwardStep):
    step_sche = [TargetS+(i+1)*ForwardStep, 2.5, MC_step]
    RQAschedule.append(step_sche)

init_state = QA_init_state 

sampleset_RQA_Reverse_Pause_Forward = sampler.sample_qubo(QUBO, schedule=RQAschedule, initial_state = init_state, num_reads=10, reinitialize_state=True) #毎回同じ初期状態からアニーリング
for state in sampleset_RQA_Reverse_Pause_Forward.record:
    selected_charts = list()
    for i in range(Nassets):
        if state[0][i]:
            selected_charts.append(Chart[i])
    portfolioChart = np.mean(selected_charts, axis=0)
    plt.plot(list(range(13)), portfolioChart, label=("Energy="+str(state[1])))

plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.text(0.2,1.8, "NForwardStep ="+'{:.2f}'.format(NForwardStep))
plt.show()

../../../_images/b8af84d0c89be1c5bf2deb29a8d58ded1c69d75c5a6c6b54236dc143f75aaab5.png

終わりに#

OpenJijを用いてReverse Quantum Annealingを実装し、ポートフォリオ最適化問題を解いてみました。このチュートリアルでは、RQAの問題定式化やスケジュール指定のやり方、そしてRQAを行う際に考慮すべきパラメータなどの説明を行いました。RQAの手法を用いることで、正しく最適解を得られることを示しました。

最適解付近にsub-optimalな解が多く存在する他の問題に関しても、同様の手法でより良い解を求めることができます。通常の量子アニーリングで局所解に囚われた場合には、このようにReverse Quantum Annealingを試して見ると解決できるかもしれません。

また、例えばスケジュールの変化が線形関数から非線形な形にした場合の影響など、RQAについてこのチュートリアルで議論しなかった部分もありますが、このチュートリアルにあるコードを変更することそれらを簡単に実行できます。興味がある方は是非試してみてください。

付録A シミュレーションの結果が上手くいかない場合#

このチュートリアルで使用された銘柄セットの生成コードは、必ずしも構成が「良い」銘柄を生成する保証はありません。そのため、場合によって偏った分布を持ったセットに対して実験する可能性もあります。その時には、遺伝的アルゴリズム計算が非常に長い実行時間になることや、チュートリアルがデフォルトで使用した $s$ や $\beta$ などのパラメータでRQAが収束しないこともあり得ます。そうした場合は銘柄セットを再生成するか、手動でRQAのパラメータ調整を行って最適解に収束するようにすると良いでしょう。

付録B DwaveマシンでRQA実験をする場合のコード#

Dwaveマシンにおいてもこのチュートリアルが実行した手法でRQAを実行することができます。ここでは参考としてそのサンプルコードを掲載します。実装及びシミュレーションと実機の違いでスケジュールの設定方法や引数が異なりますが、基本的には同じような過程となります。詳細はDwave公式サイトなどにあるドキュメントを参考にすると良いでしょう。また実機では現実のノイズなどによる影響が見られやすいため、通常のアニーリングとRQAによる結果の違いは見られやすくなります。

from dwave.system import DWaveSampler, EmbeddingComposite

token = '*** your user token ***'
endpoint = '*** your dwave endpoint***' #'https://cloud.dwavesys.com/sapi/' as defaults

dw_sampler = DWaveSampler(solver='Advantage_system4.1', token=token) #Choose your dwave machine/simulator
sampler = EmbeddingComposite(dw_sampler)

Nassets = 48


# RQA schedule
timing = (0,1,2,3)#各フェーズの開始と終了時刻、フェーズの数を増やしても問題ない
Ratio = (1.0,0.38,0.38,1.0)#各フェーズが変わる時のs
schedule = list(zip(timing,Ratio))#スケジュールにまとめる
plt.plot(timing,Ratio)
plt.show()

#Create QUBO
QUBO = np.random.rand(Nassets**2).reshape(Nassets, Nassets)
for i in  range(Nassets):
    for j in range(Nassets):
        QUBO[i][j] = PairwiseCorrMat[i][j]
for i in range(Nassets):
    QUBO[i][i] = QUBO[i][i] + SR_list[i]

import matplotlib.pyplot as plt
plt.imshow(QUBO)
plt.colorbar()
plt.show()

#FQA
sampleset = sampler.sample_qubo(QUBO,num_reads=10)
print(sampleset.record)

min_forword = 0
for result in sampleset.record:
    if result[1] < min_forword:
        min_forword = result[1]
        best_forword = result[0]
selected_charts = list()
for i in range(Nassets):
    if best_forword[i]:
        selected_charts.append(Chart[i])
portfolioChart_FQA = np.mean(selected_charts, axis=0)
plt.plot(list(range(13)), portfolioChart_FQA,color="r",label="Forward Annealing")

#RQA
sampleset_RQA = sampler.sample_qubo(QUBO,num_reads=10,  anneal_schedule=schedule, initial_state = QA_init_state)
print(sampleset_RQA.record)

min_RQA = 0
for result in sampleset_RQA.record:
    if result[1] < min_RQA:
        min_RQA = result[1]
        best_RQA = result[0]
selected_charts = list()
for i in range(Nassets):
    if best_RQA[i]:
        selected_charts.append(Chart[i])
portfolioChart_RQA = np.mean(selected_charts, axis=0)
plt.plot(list(range(13)), portfolioChart_RQA,color="b",label="Reverse Annealing")
plt.xlabel("Month", loc="right")
plt.ylabel("Portofolio Asset Amount", loc="top")
plt.legend()
plt.show()

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[21], line 1
----> 1 from dwave.system import DWaveSampler, EmbeddingComposite
      3 token = '*** your user token ***'
      4 endpoint = '*** your dwave endpoint***' #'https://cloud.dwavesys.com/sapi/' as defaults

ModuleNotFoundError: No module named 'dwave.system'

参考文献#

Harry Markowitz, “Portfolio selection”, The journal of finance, 7(1):77–91 (1952)
Davide Venturelli, Alexei Kondratyev, “Reverse Quantum Annealing Approach to Portfolio Optimization Problems”, Quantum Machine Intelligence volume 1, pages17–30 (2019)
Sharpe, William F., “Mutual fund performance”, The Journal of Business 39 (1), 119-138 (1966)