A4 - 量子イジング模型¶
[1]:
import cxxjij.graph as G
#問題サイズを100とします。
N = 100
graph = G.Dense(N)
[2]:
import numpy as np
mu, sigma = 0, 1
for i in range(N):
for j in range(N):
#Jijの値が大きくなりすぎてしまうので、全体の係数を1/Nしています。
graph[i,j] = 0 if i == j else np.random.normal()/N
for i in range(N):
graph[i] = np.random.normal()/N
グラフの設定方法は前章と同じです。
システムの設定 横磁場イジング模型¶
今回はシステムに横磁場イジング模型
を用います。
\(\Gamma\)は固定されたまま、\(\beta\)、\(s\)を変化させて量子モンテカルロ法を行います。 デフォルトでは鈴木・トロッター分解による量子モンテカルロ法が実装されています。
連続虚時間量子モンテカルロ法も用意してはいますが、現在試験的実装となっています。
まずはシステムを生成してみます。system.make_transverse_isingで生成できます。
[3]:
import cxxjij.system as S
mysystem = S.make_transverse_ising(graph.gen_spin(), graph, 1.0, 4)
ここで、1つ目の引数にはスピン列を、2つ目にはグラフ、3つ目には\(\Gamma\)の値、4つ目にはtrotterスライスの数を入力します。 これで、全てのtrotterスライスが graph.gen_spin()で初期化されたシステムができます。
mysystem.trotter_spinsで全てのtrotterスピンを表示します。縦方向が空間方向、横方向がtrotter方向です。 全てのtrotterスライスが同じスピンで初期化されていることがわかります。
[4]:
print(mysystem.trotter_spins)
[[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[ 1. 1. 1. 1.]]
graph.gen_spin()の代わりに上の二重Listを入れて直接trotterスピンを初期化することができます。
アルゴリズムの実行 -Updater, Algorithm-¶
Updater¶
量子モンテカルロ法に対しては、現状
SingleSpinFlip (メトロポリス・ヘイスティング法によるスピン1つずつのアップデート)
が使用可能です。
Algorithm¶
スケジュールリスト¶
スケジュールリストは(パラメータ, モンテカルロステップ数)のリストで与えられ、横磁場イジングモデルに対しては((\(\beta\), \(s\)), モンテカルロステップ数)で与えます。例として以下のように設定してみましょう。
[5]:
schedule_list = [((10, 0.1), 10),((12, 0.3), 80),((10, 0.8), 30)]
utilityにあるmake_transeverse_field_schedule_listを使うとより便利です。[6]:
import cxxjij.utility as U
schedule_list = U.make_transverse_field_schedule_list(10, 20, 10)
print(schedule_list)
[((beta: 10.000000, s: 0.000000) mcs: 20), ((beta: 10.000000, s: 0.111111) mcs: 20), ((beta: 10.000000, s: 0.222222) mcs: 20), ((beta: 10.000000, s: 0.333333) mcs: 20), ((beta: 10.000000, s: 0.444444) mcs: 20), ((beta: 10.000000, s: 0.555556) mcs: 20), ((beta: 10.000000, s: 0.666667) mcs: 20), ((beta: 10.000000, s: 0.777778) mcs: 20), ((beta: 10.000000, s: 0.888889) mcs: 20), ((beta: 10.000000, s: 1.000000) mcs: 20)]
上の例では\(\beta=10\)で固定しながら\(s=0\)から\(s=1\)まで、各パラメータで20モンテカルロステップ計算しながら10段階で\(s\)を変えていく設定例です。計200モンテカルロステップの計算を行います。 \(s\)の変化についてはMorita, Nishimori (2008)の手法を適用しています。
Algorithmの実行¶
続いて、Algorithmを実行します。前章と全く同じように書けます。
[7]:
import cxxjij.algorithm as A
A.Algorithm_SingleSpinFlip_run(mysystem, schedule_list)
[8]:
energies = []
def callback_log_energy(system, t):
#graphは以前にGraphモジュールにて定義したオブジェクトです
#各trotterスライスの平均値から、古典スピンの0、1を決めます。
classical_spin = [-1 if np.mean(s)<0 else 1 for s in system.trotter_spins[:-1]] #最後のスピンは補助スピンのため、除く
energies.append(graph.calc_energy(classical_spin))
このcallbackを用いて同じAlgorithmを実行します。
[9]:
#スケジュールをもっと長く取ります (計20000モンテカルロステップ)
schedule_list = U.make_transverse_field_schedule_list(10, 200, 100)
A.Algorithm_SingleSpinFlip_run(mysystem, schedule_list, callback_log_energy)
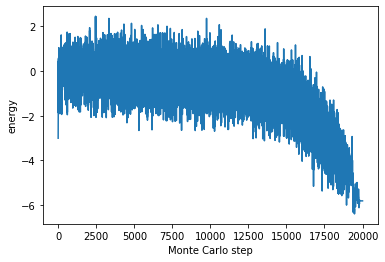
記録したシステムのエネルギーを、横軸をモンテカルロステップ、縦軸をエネルギーでプロットすると次のようになります。
[ ]:
!pip install matplotlib
[10]:
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(range(len(energies)), energies)
plt.xlabel('Monte Carlo step')
plt.ylabel('energy')
plt.show()
結果の取得 -Result-¶
result.get_solutionsで計算結果である古典スピンを取得します。この関数は最適化問題を解く観点にフォーカスを当てているため、trotterスライスの中でもっともエネルギーが低いスピン列を返します。
[11]:
import cxxjij.result as R
print(R.get_solution(mysystem))
[1, 1, 1, 1, -1, 1, -1, 1, -1, -1, -1, 1, 1, -1, 1, -1, 1, -1, -1, -1, -1, 1, -1, 1, 1, -1, 1, 1, 1, 1, -1, 1, 1, 1, 1, -1, -1, 1, 1, -1, -1, 1, -1, -1, 1, -1, -1, 1, 1, 1, 1, -1, 1, 1, -1, 1, 1, -1, 1, -1, 1, 1, 1, 1, 1, -1, -1, 1, -1, -1, 1, 1, -1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1, 1, 1, -1, 1]
C++ core interface¶
#include <graph/all.hpp>
#include <system/all.hpp>
#include <updater/all.hpp>
#include <algorithm/all.hpp>
#include <result/all.hpp>
#include <utility/schedule_list.hpp>
#include <utility/random.hpp>
#include <random>
#include <iostream>
using namespace openjij;
int main(void){
//generate dense graph with size N=100
constexpr std::size_t N = 100;
auto dense = graph::Dense<double>(N);
//generate random engine
auto rand_engine = std::mt19937(0x1234);
//of course you can specify another random generator that is compatible with C++ random generator, say utility::Xorshift,
//auto rand_engine = utility::Xorshift(0x1234);
//Gaussian distribution
auto gauss = std::normal_distribution<>{0, 1};
//set interactions
for(std::size_t i=0; i<N; i++){
for(std::size_t j=0; j<N; j++){
dense.J(i, j) = (i == j) ? 0 : gauss(rand_engine)/N;
}
}
//set local fields
for(std::size_t i=0; i<N; i++){
dense.h(i) = gauss(rand_engine);
}
//create transverse Ising system
auto system = system::make_transverse_ising(dense.gen_spin(rand_engine), dense, 1.0, 4);
//generate schedule list
auto schedule_list = utility::make_transverse_field_schedule_list(10, 20, 10);
//do annealing (updater: SingleSpinFlip)
algorithm::Algorithm<updater::SingleSpinFlip>::run(system, rand_engine, schedule_list);
//show spins
std::cout << "The result spins are [";
for(auto&& elem : result::get_solution(system)){
std::cout << elem << " ";
}
std::cout << "]" << std::endl;
}