6-Machine Learning (QBoost) with Quantum Annealing¶
In this section, we describe machine lerning (ML) as an example of an application of quantum annealing (QA) optimization.
Clustering¶
Clustering is the task of deviding given set of data into \(n\) clusters (\(n\) is our input). For the sake of simplicity, let us consider the number of cluster is 2 in this time.
Importing the required libraries¶
We import scikit-learn library for ML.
[1]:
# import libraries
import numpy as np
from matplotlib import pyplot as plt
from sklearn import cluster
import pandas as pd
from scipy.spatial import distance_matrix
from pyqubo import Array, Constraint, Placeholder, solve_qubo
import openjij as oj
from sklearn.model_selection import train_test_split
Make artificial data¶
In this case, let us generate linearly separable data in a two-dimensional plane artificially.
[2]:
data = []
label = []
for i in range(100):
# generate 0 to 1 random number
p = np.random.uniform(0, 1)
# set class 1 when certain condition are met, and -1 when it are not met
cls =1 if p>0.5 else -1
# create random numbers following a normal distribution
data.append(np.random.normal(0, 0.5, 2) + np.array([cls, cls]))
label.append(cls)
# formatted as a DataFrame
df1 = pd.DataFrame(data, columns=["x", "y"], index=range(len(data)))
df1["label"] = label
[3]:
# visualize dataset
df1.plot(kind='scatter', x="x", y="y")
plt.show()
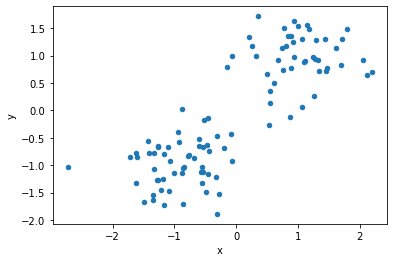
We demonstrate clustering by minimizing the following Hamiltonians.
Where \(i, j\) is sample No., \(d_{i, j}\) is a distance between \(i\) and \(j\), \(\sigma_i=\{-1,1\}\) is spin variable that indicates whether \(i\) belong to one of the two clusters.
Each term of this Hamiltonian sum behaves as follows.
0 for $:nbsphinx-math:sigma_i = \sigma_j $
\(d_{i,j}\) for $:nbsphinx-math:sigma_i \neq `:nbsphinx-math:sigma`_j $
Note that minus of R.H.S., Hamiltonian means the problem is “Choosing pairs of \(\{\sigma _1, \sigma _2 \ldots \}\) that maximizes the distance between the samples of different classes”.
Clustering with PyQUBO¶
At first, we formulate the Hamiltonian in PyQUBO. Second, we execute simulated annealing (SA) with solve_qubo.
[6]:
def clustering_pyqubo(df):
# set distance matrix
d_ij = distance_matrix(df, df)
# set spin variables
spin = Array.create("spin", shape= len(df), vartype="SPIN")
# set the total Hamiltonian
H = - 0.5* sum(
[d_ij[i,j]* (1 - spin[i]* spin[j]) for i in range(len(df)) for j in range(len(df))]
)
# compile
model = H.compile()
# convert to QUBO
qubo, offset = model.to_qubo()
# solve with SA
raw_solution = solve_qubo(qubo, num_reads=10)
# decode for easier analysis
decoded_samples = model.decode_sample(raw_solution, vartype="SPIN")
# extract label
labels = [decoded_samples.array("spin", idx) for idx in range(len(df))]
return labels
We execute and check a solution.
[7]:
labels =clustering_pyqubo(df1[["x", "y"]])
print("label", labels)
label [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0]
<ipython-input-6-79e62663b237>:15: DeprecationWarning: Call to deprecated function (or staticmethod) solve_qubo. (You should use simulated annealing sampler of dwave-neal directly.) -- Deprecated since version 0.4.0.
raw_solution = solve_qubo(qubo, num_reads=10)
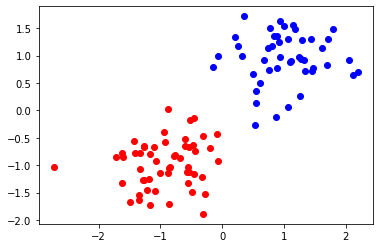
Let us visualize the result.
[8]:
for idx, label in enumerate(labels):
if label:
plt.scatter(df1.loc[idx]["x"], df1.loc[idx]["y"], color="b")
else:
plt.scatter(df1.loc[idx]["x"], df1.loc[idx]["y"], color="r")
Clustering with OpenJij solver¶
Next, we introduce clustering with OpenJij solver and use PyQUBO to formulate QUBO.
[9]:
def clustering_openjij(df):
# set distance matrix
d_ij = distance_matrix(df, df)
# set spin variables
spin = Array.create("spin", shape= len(df), vartype="SPIN")
# set total Hamiltonian
H = - 0.5* sum(
[d_ij[i,j]* (1 - spin[i]* spin[j]) for i in range(len(df)) for j in range(len(df))]
)
# compile
model = H.compile()
# convert to QUBO
qubo, offset = model.to_qubo()
# set OpenJij SA sampler
sampler = oj.SASampler(num_reads=10, num_sweeps=100)
# solve with above sampler
response = sampler.sample_qubo(qubo)
# extract raw data
raw_solution = dict(zip(response.indices, response.states[np.argmin(response.energies)]))
# decode for easier analysis
decoded_samples= model.decode_sample(raw_solution, vartype="SPIN")
# extract labels
labels = [int(decoded_samples.array("spin", idx) ) for idx in range(len(df))]
return labels, sum(response.energies)
We execute and check a solution.
[10]:
labels, energy =clustering_openjij(df1[["x", "y"]])
print("label", labels)
print("energy", energy)
label [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0]
energy -139358.74510750096
And also we visualize the result.
[11]:
for idx, label in enumerate(labels):
if label:
plt.scatter(df1.loc[idx]["x"], df1.loc[idx]["y"], color="b")
else:
plt.scatter(df1.loc[idx]["x"], df1.loc[idx]["y"], color="r")
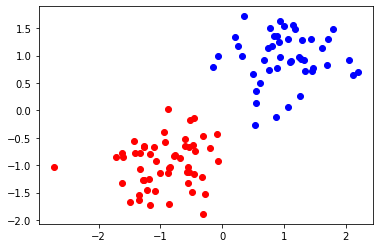
We can get a same figure as using PyQUBO SA.
QBoost¶
QBoost is a one of the ensamble learning using QA. Ensamble learning involves preparing a number of weak predictors and combining the results of each of these predictors to obtain the final prediction result.
QBoost uses QA to optimize the best combination of learners for a given training data. We handle classification problem in this time.
We define that the set of \(D\) training data are \(\{\vec x^{(d)}\}(d=1, ..., D)\), corresponding label are \(\{y^{(d)}\}(d=1, ..., D), y^{(d)}\in \{-1, 1\}\) and the (function) set of \(N\) weak learner is \(\{C_i\}(i=1, ..., N)\). For some data \(\vec x^{(d)}\), \(C_i(\vec x^{(d)})\in \{-1, 1\}\).
Based on the definitions above, the classification labels are as follows.
Where \(w_i\in\{0, 1\} (i=1, ..., N)\), is a weight of each predictor (bool value to adopt or not adopt the predictor for the final prediction).QBoost optimizes the combination of \(w_i\) so that prediction matches the training data while erasing the number of weak learners.
Hamiltonian in this problem is as follows.
The first term represents the difference between weak classifier and the correct label. The second term represents a degree of the number of weak classifier to be employed in the final classifier. \(\lambda\) is the regularization parameter that adjust how much the number of weak classifiers affects the total Hamiltonian.
We optimize this Hamiltonian by recognizing the first term as a cost (objective function) and the second term as a constraint.Minimizing with QA allows us to obtain a combination of weak classifiers that best fits the training data.
Scripts¶
Let us try QBoost. We use the cancer identification dataset from scikit-learn for training data. For simplicity, we will only use two character types for training: “0” and “1”.
[12]:
# import libraries
import pandas as pd
from scipy import stats
from sklearn import datasets
from sklearn import metrics
[13]:
# load data
cancerdata = datasets.load_breast_cancer()
# set the number of training data & test data
num_train = 450
In this time, we consider that feature of noise exists.
[14]:
data_noisy = np.concatenate((cancerdata.data, np.random.rand(cancerdata.data.shape[0], 30)), axis=1)
print(data_noisy.shape)
(569, 60)
[15]:
# convert from label {0, 1} to {-1, 1}
labels = (cancerdata.target-0.5) * 2
[16]:
# divide dataset to training and test
X_train = data_noisy[:num_train, :]
X_test = data_noisy[num_train:, :]
y_train = labels[:num_train]
y_test = labels[num_train:]
[17]:
# from the result of weak learnor
def aggre_mean(Y_list):
return ((np.mean(Y_list, axis=0)>0)-0.5) * 2
Set of Weak Learner¶
We make weak learner with scikit-learn. In this time, we choose decision stump. Desision stump is a single-layer decision tree. As it will be used as a weak classifier, the features to be used for segmentation are selected randomly (it’s a good understanding that we execute single-layer of random forest).
[18]:
# import required libraries
from sklearn.tree import DecisionTreeClassifier as DTC
# set the number of weak classifier
num_clf = 32
# set the number of ensembles to be taken out for one sample in bootstrap sampling
sample_train = 40
# set model
models = [DTC(splitter="random",max_depth=1) for i in range(num_clf)]
for model in models:
# extract randomly
train_idx = np.random.choice(np.arange(X_train.shape[0]), sample_train)
# make decision tree with variables
model.fit(X=X_train[train_idx], y=y_train[train_idx])
y_pred_list_train = []
for model in models:
# execute prediction with model
y_pred_list_train.append(model.predict(X_train))
y_pred_list_train = np.asanyarray(y_pred_list_train)
y_pred_train =np.sign(y_pred_list_train)
We look accuracy of all weak learner as the final classifier. Henceforth, we refer to this combination as baseline.
[19]:
y_pred_list_test = []
for model in models:
# execute with test data
y_pred_list_test.append(model.predict(X_test))
y_pred_list_test = np.array(y_pred_list_test)
y_pred_test = np.sign(np.sum(y_pred_list_test,axis=0))
# compute score of prediction accuracy
acc_test_base = metrics.accuracy_score(y_true=y_test, y_pred=y_pred_test)
print(acc_test_base)
0.9663865546218487
[20]:
# set class of QBoost
class QBoost():
def __init__(self, y_train, ys_pred):
self.num_clf = ys_pred.shape[0]
# set binary variables
self.Ws = Array.create("weight", shape = self.num_clf, vartype="BINARY")
# set hyperparameter with PyQUBO Placeholder
self.param_lamda = Placeholder("norm")
# set combination of weak classifier Hamiltonian
self.H_clf = sum( [ (1/self.num_clf * sum([W*C for W, C in zip(self.Ws, y_clf)])- y_true)**2 for y_true, y_clf in zip(y_train, ys_pred.T)
])
# set normalization term as a constraint
self.H_norm = Constraint(sum([W for W in self.Ws]), "norm")
# set total Hamiltonian
self.H = self.H_clf + self.H_norm * self.param_lamda
# compile
self.model = self.H.compile()
# set function for converting to QUBO
def to_qubo(self, norm_param=1):
# set value of hyperparameter
self.feed_dict = {'norm': norm_param}
return self.model.to_qubo(feed_dict=self.feed_dict)
[21]:
qboost = QBoost(y_train=y_train, ys_pred=y_pred_list_train)
# make QUBO with lambda=3
qubo = qboost.to_qubo(3)[0]
Execute QBoost with D-Wave Sampler¶
[20]:
# import required libraries
from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite
[25]:
# set DwaveSampler with token yourself
dw = DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi/',
token='xxxx',
solver='DW_2000Q_VFYC_6')
# embed on chimeragraph
sampler = EmbeddingComposite(dw)
---------------------------------------------------------------------------
SolverAuthenticationError Traceback (most recent call last)
<ipython-input-25-d66cc9ab60bd> in <module>
1 dw = DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi/',
2 token='xxxx',
----> 3 solver='DW_2000Q_VFYC_6')
4 sampler = EmbeddingComposite(dw)
~/.local/share/virtualenvs/OpenJijTutorial-bCQ9CWHW/lib/python3.7/site-packages/dwave/system/samplers/dwave_sampler.py in __init__(self, failover, retry_interval, **config)
163
164 self.client = Client.from_config(**config)
--> 165 self.solver = self.client.get_solver()
166
167 self.failover = failover
~/.local/share/virtualenvs/OpenJijTutorial-bCQ9CWHW/lib/python3.7/site-packages/dwave/cloud/client.py in get_solver(self, name, refresh, **filters)
1077 try:
1078 logger.debug("Fetching solvers according to filters=%r", filters)
-> 1079 return self.get_solvers(refresh=refresh, **filters)[0]
1080 except IndexError:
1081 raise SolverNotFoundError("Solver with the requested features not available")
~/.local/share/virtualenvs/OpenJijTutorial-bCQ9CWHW/lib/python3.7/site-packages/dwave/cloud/client.py in get_solvers(self, refresh, order_by, **filters)
990
991 # filter
--> 992 solvers = self._fetch_solvers(**query)
993 solvers = [s for s in solvers if all(p(s) for p in predicates)]
994
~/.local/share/virtualenvs/OpenJijTutorial-bCQ9CWHW/lib/python3.7/site-packages/dwave/cloud/utils.py in wrapper(*args, **kwargs)
404 val = data.get('val')
405 else:
--> 406 val = fn(*args, **kwargs)
407 self.cache[key] = dict(expires=now+self.maxage, val=val)
408
~/.local/share/virtualenvs/OpenJijTutorial-bCQ9CWHW/lib/python3.7/site-packages/dwave/cloud/client.py in _fetch_solvers(self, name)
622
623 if response.status_code == 401:
--> 624 raise SolverAuthenticationError
625
626 if name is not None and response.status_code == 404:
SolverAuthenticationError: Token not accepted for that action.
[26]:
# compute DWaveSampler
sampleset = sampler.sample_qubo(qubo, num_reads=100)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-26-5a2ab598e52b> in <module>
1 # D-Waveサンプラーで計算
----> 2 sampleset = sampler.sample_qubo(qubo, num_reads=100)
NameError: name 'sampler' is not defined
[27]:
# check the result
print(sampleset)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-27-9a5afadcc2dd> in <module>
1 # 結果の確認
----> 2 print(sampleset)
NameError: name 'sampleset' is not defined
[28]:
# decode each computation result with PyQUBO
decoded_solutions = []
brokens = []
energies =[]
decoded_sol = qboost.model.decode_dimod_response(sampleset, feed_dict=qboost.feed_dict)
for d_sol, broken, energy in decoded_sol:
decoded_solutions.append(d_sol)
brokens.append(broken)
energies.append(energy)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-28-6c74ef10896c> in <module>
4 energies =[]
5
----> 6 decoded_sol = qboost.model.decode_dimod_response(sampleset, feed_dict=qboost.feed_dict)
7 for d_sol, broken, energy in decoded_sol:
8 decoded_solutions.append(d_sol)
NameError: name 'sampleset' is not defined
Let us check the accuracy in the training/validation data when using a combination of weak classifiers obtained by D-Wave.
[29]:
accs_train_Dwaves = []
accs_test_Dwaves = []
for decoded_solution in decoded_solutions:
idx_clf_DWave=[]
for key, val in decoded_solution["weight"].items():
if val == 1:
idx_clf_DWave.append(int(key))
y_pred_train_DWave = np.sign(np.sum(y_pred_list_train[idx_clf_DWave, :], axis=0))
y_pred_test_DWave = np.sign(np.sum(y_pred_list_test[idx_clf_DWave, :], axis=0))
acc_train_DWave = metrics.accuracy_score(y_true=y_train, y_pred=y_pred_train_DWave)
acc_test_DWave= metrics.accuracy_score(y_true=y_test, y_pred=y_pred_test_DWave)
accs_train_Dwaves.append(acc_train_DWave)
accs_test_Dwaves.append(acc_test_DWave)
We make a graph with energy on the horizontal axis and accuracy on the vertical axis.
[43]:
plt.figure(figsize=(12, 8))
plt.scatter(energies, accs_train_Dwaves, label="train" )
plt.scatter(energies, accs_test_Dwaves, label="test")
plt.xlabel("energy: D-wave")
plt.ylabel("accuracy")
plt.title("relationship between energy and accuracy")
plt.grid()
plt.legend()
plt.show()
[44]:
print("base accuracy is {}".format(acc_test_base))
print("max accuracy of QBoost is {}".format(max(accs_test_Dwaves)))
print("average accuracy of QBoost is {}".format(np.mean(np.asarray(accs_test_Dwaves))))
base accuracy is 0.9411764705882353
max accuracy of QBoost is 0.957983193277311
average accuracy of QBoost is 0.9398183515830576
D-Wave samplig can perform hundreds or more sampling in a short period. It is possible to create a more accurate classifier than a baseling if you use the results that maximiza accuracy.
[ ]: